高中数学解答题

（本小题满分10分）选修4－4 ：坐标系与参数方程
在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为
cos（）=1，M,N分别为C与x轴，y轴的交点。
（1）写出C的直角坐标方程，并求M,N的极坐标；
（2）设MN的中点为P，求直线OP的极坐标方程。

本小题满分10分）选修4－1：几何证明选讲     
已知ABC中，AB="AC, " D是 ABC外接圆劣弧AC弧上的点（不与点A,C重合），延长BD至E。
（1）        求证：AD的延长线平分CDE；
（2）        若BAC=30°，ABC中BC边上的高为2+，求ABC外接圆的面积。

（本小题满分12分）
设直线与抛物线交于不同两点A、B，F为抛物线的焦点。
（1）求的重心G的轨迹方程；
（2）如果的外接圆的方程。

已知数列是首项的等比数列，其前项和中，，成等差数列，
（1）求数列的通项公式；
（2）设，若，求证：．

己知在锐角ΔABC中，角所对的边分别为，且
（Ⅰ）求角大小；
（Ⅱ）当时，求的取值范围.

．已知圆，直线过定点 A (1，0)．
（1）若与圆C相切，求的方程；
（2）若的倾斜角为，与圆C相交于P，Q两点，求线段PQ的中点M的坐标；
（3）若与圆C相交于P，Q两点，求△CPQ面积的最大值

如图，已知中，，斜边上的高，以为折痕，将折 起，使为直角。
（1）求证：平面平面；（2）求证：
（3） 求点到平面的距离；（4） 求点到平面的距离；
　　　　　　　　　　　　　　　　　　　　

已知直线l过点P（3，4）
(1)它在y轴上的截距是在x轴上截距的2倍，求直线l的方程.
(2)若直线l与轴，轴的正半轴分别交于点，求的面积的最小值.

在三棱锥中，
（1）证明：；
（2）求三棱锥的体积

如图，在四面体中，，点分别是的中点． 求证：
（1）直线平面；
（2）平面平面．

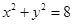已知圆内有一点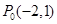，AB为过点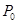且倾斜角为α的弦，
（1）当α=135º时，求直线AB的方程
（2）若弦AB被点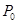平分，求直线AB的方程。

（本小题满分10分）
某市公租房的房源位于A，B，C三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的求该市的任4位申请人中：
（Ⅰ）恰有2人申请A片区房源的概率；
（Ⅱ）申请的房源所在片区的个数的分布列与期望

（本小题满分10分）
已知，（其中）
⑴求及；
⑵试比较与的大小，并说明理由．

．选修4—4：坐标系与参数方程
椭圆中心在原点，焦点在轴上。离心率为，点是椭圆上的一个动点，
若的最大值为，求椭圆的标准方程．

选修4﹣2：矩阵与变换
已知二阶矩阵对应的变换将点（﹣2，1）变换成点（0，b），求实数a，b的值．