据预测,某旅游景区游客人数在 至
至 人之间,游客人数
人之间,游客人数 (人)与游客的消费总额
(人)与游客的消费总额 (元)之间近似地满足关系:
(元)之间近似地满足关系:
(Ⅰ)若该景区游客消费总额不低于 元时,求景区游客人数的范围
元时,求景区游客人数的范围
(Ⅱ)当景区游客的人数为多少人时,游客的人均消费最高?并求游客的人均最高消费额
某公司通过报纸和电视两种方式做销售某种商品的广告,根据统计资料,销售收入R(万元)与报纸广告费用x1(万元)及电视广告费用x2(万元)之间的关系有如下经验公式:R=-2x12-x22+13x1+11x2-28.
(1)若提供的广告费用共为5万元,求最优广告策略.(即收益最大的策略,其中收益=销售收入-广告费用)
(2)在广告费用不限的情况下,求最优广告策略
已知二次函数 的最小值为1,且
的最小值为1,且 .
.
(1)求 的解析式;
的解析式;
(2)若 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)在区间 上,
上, 的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数 的取值范围.
的取值范围.
某上市股票在30天内每股的交易价格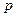 (元)与时间
(元)与时间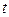 (天)组成有序数对
(天)组成有序数对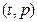 ,点
,点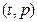 落在图中的两条线段上.该股票在30天内(包括30天)的日交易量
落在图中的两条线段上.该股票在30天内(包括30天)的日交易量 (万股)与时间
(万股)与时间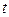 (天)的部分数据如下表所示:
(天)的部分数据如下表所示:
第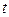 天 天 |
4 |
10 |
16 |
22 |
 (万股) (万股) |
36 |
30 |
24 |
18 |
(1)根据提供的图象,写出该种股票每股的交易价格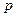 (元)与时间
(元)与时间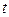 (天)所满足的函数关系式;
(天)所满足的函数关系式;
(2)根据表中数据确定日交易量 (万股)与时间
(万股)与时间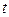 (天)的一次函数关系式;
(天)的一次函数关系式;
(3)用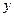 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出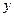 关于
关于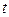 的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
已知椭圆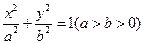 的两个焦点为F1、F2,椭圆上一点
的两个焦点为F1、F2,椭圆上一点 满足
满足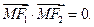
(1)求椭圆的方程;
(2)若直线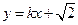 与椭圆恒有两上不同的交点A、B,且
与椭圆恒有两上不同的交点A、B,且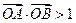 (O是坐标原点),求k的范围。
(O是坐标原点),求k的范围。
试题篮
()