“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取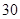 名路人进行了问卷调查,得到了如下列联表:
名路人进行了问卷调查,得到了如下列联表:
| |
男性 |
女性 |
合计 |
| 反感 |
10 |
|
|
| 不反感 |
|
8 |
|
| 合计 |
|
|
30 |
已知在这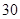 人中随机抽取
人中随机抽取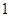 人抽到反感“中国式过马路 ”的路人的概率是
人抽到反感“中国式过马路 ”的路人的概率是 .
.
(Ⅰ)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料判断是否有95%的把握认为反感“中国式过马路 ”与性别有关?
(Ⅱ)若从这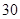 人中的女性路人中随机抽取
人中的女性路人中随机抽取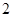 人参加一活动,记反感“中国式过马路”的人数为
人参加一活动,记反感“中国式过马路”的人数为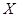 ,求
,求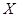 的分布列.
的分布列.
附: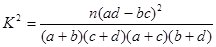 ,其中
,其中 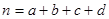
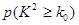 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
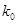 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
在直角坐标系 中,设动点
中,设动点 到定点
到定点 的距离与到定直线
的距离与到定直线 的距离相等,记
的距离相等,记 的轨迹为
的轨迹为 .又直线
.又直线 的一个方向向量
的一个方向向量 且过点
且过点 ,
, 与
与 交于
交于 两点,求
两点,求 的长.
的长.
已知函数
,其中常数
(1)令
,判断函数
的奇偶性,并说明理由;
(2)令
,将函数
的图象向左平移个
单位,再向上平移1个单位,得到函数
的图象,对任意
,求
在区间
上零点个数的所有可能值.
设
是公比为
的等比数列.
(Ⅰ) 推导
的前
项和公式;
(Ⅱ) 设
, 证明数列
不是等比数列.
某小组共有
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
| 身高 |
1.69 |
1.73 |
1.75 |
1.79 |
1.82 |
| 体重指标 |
19.2 |
25.1 |
18.5 |
23.3 |
20.9 |
(Ⅰ)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(Ⅱ)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在
中的概率.
如图,从参加环保知识竞赛的学生中抽出 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1) 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率( 分及以上为及格)
分及以上为及格)
第 届亚运会于
届亚运会于 年
年 月
月 日至
日至 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了 名男志愿者和
名男志愿者和 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有 人和
人和 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
根据以上数据完成以下 列联表:
列联表:
| |
喜爱运动 |
不喜爱运动 |
总计 |
| 男 |
10 |
|
16 |
| 女 |
6 |
|
14 |
| 总计 |
|
|
30 |
(2)能否在犯错误的概率不超过 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有 人会外语),抽取
人会外语),抽取 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?
附:K2=
| P(K2≥k) |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
试题篮
()