已知函数
的周期为
,图象的一个对称中心为
,将函数
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
单位长度后得到函数
的图象。
(Ⅰ)求函数
与
的解析式
(Ⅱ)是否存在
,使得
按照某种顺序成等差数列?若存在,请确定
的个数,若不存在,说明理由;
(Ⅲ)求实数
与正整数
,使得
在
内恰有2013个零点.
如图,在四棱柱 中,侧棱 底面 ,

(Ⅰ)求证: 平面 .
(Ⅱ)若直线 与平面 所成角的正弦值为 ,求 的值.
(Ⅲ)现将与四棱柱 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出 的解析式。(直接写出答案,不必说明理由).
设函数
,其中
,区间
.
(Ⅰ)求
的长度(注:区间
的长度定义为
;
(Ⅱ)给定常数
,当
时,求
长度的最小值.
设函数
.
(Ⅰ)求
的最小值,并求使
取得最小值的 的集合;
的集合;
(Ⅱ)不画图,说明函数
的图像可由
的图象经过怎样的变化得到.
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.

(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
已知函数
(
为自然对数的底数)
(Ⅰ)若曲线
在点
处的切线平行于
轴,求
的值;
(Ⅱ)求函数
的极值;
(Ⅲ)当
时,若直线
与曲线
没有公共点,求
的最大值.
如图,抛物线
的焦点为
,准线
与
轴的交点为
.点
在抛物线
上,以
为圆心,
为半径作圆,设圆
与准线
交于不同的两点
,
.
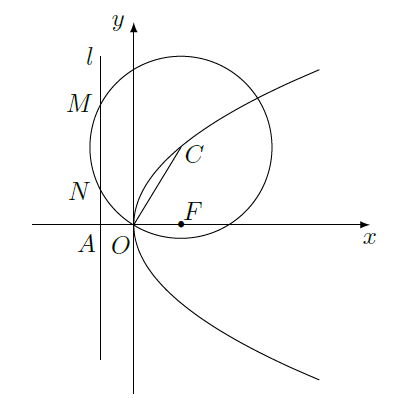
(I)若点
的纵坐标为2,求
;
(II)若
,求圆
的半径.
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在"25周岁以上(含25周岁)"和"25周岁以下"分为两组,再将两组工人的日平均生产件数分为5组: , , , , ,分别加以统计,得到如图所示的频率分布直方图.

(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名"25周岁以下组"工人的概率;
(II)规定日平均生产件数不少于80件者为"生产能手",请你根据已知条件完成列联表,并判断是否有90%的把握认为"生产能手与工人所在的年龄组有关"?
附: (注:此公式也可以写成 )
| 0.100 |
0.050 |
0.010 |
0.001 |
|
| 2.706 |
3.841 |
6.635 |
10.828 |
考察某种药物预防甲型H1N1流感的效果,进行动物试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(Ⅰ)根据所给样本数据完成下面2×2列联表;
(Ⅱ)请问能有多大把握认为药物有效?
| |
不得流感 |
得流感 |
总计 |
| 服药 |
|
|
|
| 不服药 |
|
|
|
| 总计 |
|
|
|
(参考数据: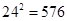 )
)
 的三个内角A,B,C所对的边分别为a,b,c, 向量
的三个内角A,B,C所对的边分别为a,b,c, 向量
 且
且
(Ⅰ)求 的大小;
的大小;
(Ⅱ)现给出下列四个条件:① ②
② ③
③ ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 ,求出你所确定的
,求出你所确定的 的面积.
的面积.
某初级中学共有学生2000名,各年级男、女生人数如下表:
| |
初一年级 |
初二年级 |
初三年级 |
| 女生 |
373 |
 |
 |
| 男生 |
377 |
370 |
 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
试题篮
()