高中数学解答题

已知函数 $f\left(x\right)=|3x+1|-2|x-1|$ ．

（1）画出 $y=f\left(x\right)$ 的图像；

（2）求不等式 $f\left(x\right)>f(x+1)$ 的解集．

已知函数 $f\left(x\right)=e^x+a{x}^2-x$ .

（1）当 a=1时，讨论 f（ x）的单调性；

（2）当 x≥0时， f（ x）≥ $\frac{1}{2}$ x ³+1，求 a的取值范围.

已知A、B分别为椭圆E： $\frac{x^2}{a^2}+y^2=1$（a>1）的左、右顶点，G为E的上顶点， $\overrightarrow{\mathit{AG}}\cdot \overrightarrow{\mathit{GB}}=8$，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D．

（1）求E的方程；

（2）证明：直线CD过定点.

已知函数 $f\left(x\right)=a{e}^{x-1}-\mathit{ln}x+\mathit{ln}a$．

（1）当 $a=e$时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积；

（2）若f（x）≥1，求a的取值范围．

甲口袋中装有2个黑球和1个白球，乙口袋中装有3个白球．现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复n次这样的操作，记甲口袋中黑球个数为X_n，恰有2个黑球的概率为p_n，恰有1个黑球的概率为q_n．

（1）求p₁·q₁和p₂·q₂；

（2）求2p_n+q_n与2p_n-1+q_n-1的递推关系式和X_n的数学期望E(X_n)(用n表示) ．

已知数列 $\left\{a_n\right\}(n\in N^{*})$的首项a₁=1，前n项和为S_n．设λ与k是常数，若对一切正整数n，均有 ${S_{n+1}}^{\frac{1}{k}}-{S_n}^{\frac{1}{k}}=\lambda {a_{n+1}}^{\frac{1}{k}}$成立，则称此数列为“λ–k”数列．

（1）若等差数列 $\left\{a_n\right\}$是“λ–1”数列，求λ的值；

（2）若数列 $\left\{a_n\right\}$是“ $\frac{\sqrt{3}}{3}-2$”数列，且a_n＞0，求数列 $\left\{a_n\right\}$的通项公式；

（3）对于给定的λ，是否存在三个不同的数列 $\left\{a_n\right\}$为“λ–3”数列，且a_n≥0?若存在，求λ的取值范围；若不存在，说明理由，

已知关于x的函数 $y=f\left(x\right),y=g\left(x\right)$与 $h\left(x\right)=\mathit{kx}+b(k,b\in R)$在区间D上恒有 $f\left(x\right)\ge h\left(x\right)\ge g\left(x\right)$．

（1）若 $f\left(x\right)=x^2+2x，g\left(x\right)=-x^2+2x，D=(-\infty ，+\infty )$，求h(x)的表达式；

（2）若 $f\left(x\right)=x^2-x+1，g\left(x\right)=\mathit{k}\mathit{ln}x，h\left(x\right)=\mathit{kx}-k,D=(0，+\infty )$，求k的取值范围；

（3）若 $f\left(x\right)=x^4-2x^2，g\left(x\right)=4x^2-8，h\left(x\right)=4\left(t^2-t\right)x-3t^4+2t^2(0<\left|\mathit{t}\right|\le \sqrt{2})，D=\left[m,\mathit{n}\right]\subseteq \left[-\sqrt{2},\sqrt{2}\right]，$求证： $n-m\le \sqrt{7}$．

已知函数 $f\left(x\right)=x^3+k\mathit{ln}x(k\in R)$， $f^{\text{'}}\left(x\right)$为 $f\left(x\right)$的导函数．

（Ⅰ）当 $k=6$时，

（i）求曲线 $y=f\left(x\right)$在点 $(1,f(1\left)\right)$处的切线方程；

（ii）求函数 $g\left(x\right)=f\left(x\right)-f^{\text{'}}\left(x\right)+\frac{9}{x}$的单调区间和极值；

（Ⅱ）当 $k⩾-3$时，求证：对任意的 $x_1,\hspace{1em}{x}_2\in [1,+\infty )$，且 $x_1>x_2$，有 $\frac{f^{\text{'}}\left(x_1\right)+f^{\text{'}}\left(x_2\right)}{2}>\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}$．

已知 $1<a\le 2$，函数 $f\left(x\right)=e^x-x-a$，其中e=2.71828…为自然对数的底数．

（Ⅰ）证明：函数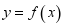在 $(0，+\infty )$上有唯一零点；

（Ⅱ）记x₀为函数在 $(0，+\infty )$上的零点，证明：

（ⅰ） $\sqrt{a-1}\le x_0\le \sqrt{2(a-1)}$；

（ⅱ） $x_{0}f(e^{x_0})\ge (e-1\left)\right(a-1)a$．

已知 $\left\{a_n\right\}$是无穷数列．给出两个性质：

①对于 $\left\{a_n\right\}$中任意两项 $a_i,a_j(i>j)$，在 $\left\{a_n\right\}$中都存在一项 $a_m$，使 $\frac{a_i^2}{a_j}=a_m$；

②对于 $\left\{a_n\right\}$中任意项 $a_n(n⩾3)$，在 $\left\{a_n\right\}$中都存在两项 $a_k,a_l(k>l)$．使得 $a_n=\frac{a_k^2}{a_l}$．

(Ⅰ)若 $a_n=n(n=1,2,\cdots )$，判断数列 $\left\{a_n\right\}$是否满足性质①，说明理由；

(Ⅱ)若 $a_n=2^{n-1}(n=1,2,\cdots )$，判断数列 $\left\{a_n\right\}$是否同时满足性质①和性质②，说明理由；

(Ⅲ)若 $\left\{a_n\right\}$是递增数列，且同时满足性质①和性质②，证明： $\left\{a_n\right\}$为等比数列.

已知函数 $f\left(x\right)=|3x+1|-2|x-1|$ ．

（1）画出 $y=f\left(x\right)$ 的图像；

（2）求不等式 $f\left(x\right)>f(x+1)$ 的解集．

已知A、B分别为椭圆E： $\frac{x^2}{a^2}+y^2=1$（a>1）的左、右顶点，G为E的上顶点， $\overrightarrow{\mathit{AG}}\cdot \overrightarrow{\mathit{GB}}=8$，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D．

（1）求E的方程；

（2）证明：直线CD过定点.

已知函数 $f\left(x\right)=\left|x-a^2\right|+|x-2a+1|$ .

（1）当 $a=2$ 时，求不等式 $f\left(x\right)⩾4$ 的解集；

（2）若 $f\left(x\right)⩾4$ ，求 a的取值范围.

已知曲线C₁，C₂的参数方程分别为C₁：（θ为参数），C₂： $\left\{\begin{array}{c}x=t+\frac{1}{t},\\ y=t-\frac{1}{t}\end{array}\right.$（t为参数）.

（1）将C₁，C₂的参数方程化为普通方程；

（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系.设C₁，C₂的交点为P，求圆心在极轴上，且经过极点和P的圆的极坐标方程.

设 a， b， c $\in$ R， a+ b+ c=0， abc=1．

（1）证明： ab+ bc+ ca<0；

（2）用max{ a， b， c}表示 a， b， c中的最大值，证明：max{ a， b， c}≥ $\sqrt[3]{4}$ ．