高中数学解答题

已知二次函数 $y=g\left(x\right)$的导函数的图像与直线 $y=2x$平行，且 $y=g\left(x\right)$在 $x=-1$处取得极小值 $m-1(m\ne 0)$．设 $f\left(x\right)=\frac{g\left(x\right)}{x}$．

（１）若曲线 $y=f\left(x\right)$上的点 $P$到点 $Q(0,2)$的距离的最小值为 $\sqrt{2}$，求 $m$的值；

（２） $k(k\in R)$如何取值时，函数 $y=f\left(x\right)-\mathit{kx}$存在零点，并求出零点．

已知曲线 $C:y=x^2$与直线 $l:x-y+2=0$交于两点 $A(x_A,y_A)$和 $B(x_B,y_B)$，且 $x_A<x_B$．记曲线 $C$在点 $A$和点 $B$之间那一段 $L$与线段 $\mathit{AB}$所围成的平面区域（含边界）为 $D$．设点 $P(s,t)$是 $L$上的任一点，且点 $P$与点 $A$和点 $B$均不重合．

（１）若点 $Q$是线段 $\mathit{AB}$的中点，试求线段 $\mathit{PQ}$的中点 $M$的轨迹方程；

（２）若曲线 $G:x^2-2\mathit{ax}+y^2-4y+a^2+\frac{51}{25}=0$与点 $D$有公共点，试求 $a$的最小值．

如下图，已知正方体 $\mathit{ABCD}-A_1{B}_1{C}_1{D}_1$的棱长为２，点Ｅ是正方形 $\mathit{BC}{C}_1{B}_1$的中心，点Ｆ、Ｇ分别是棱 $C_1{D}_1,A{A}_1$的中点．设点 $E_1,G_1$分别是点Ｅ，Ｇ在平面 $\mathit{DC}{C}_1{D}_1$内的正投影．

（１）求以Ｅ为顶点，以四边形 $\mathit{FGAE}$在平面 $\mathit{DC}{C}_1{D}_1$内的正投影为底面边界的棱锥的体积；

（２）证明：直线 $F{G}_1\perp \mathit{平面}\mathit{FE}{E}_1$；

（３）求异面直线 $E_1{G}_1与\mathit{EA}$所成角的正弦值.

根据空气质量指数API（为整数）的不同，可将空气质量分级如下表:

对某城市一年（ 365天）的空气质量进行监测，获得的API数据按照区间 $[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]$ 进行分组，得到频率分布直方图如下图.

                         

（1）求直方图中 $x$ 的值；

（2）计算一年中空气质量分别为良和轻微污染的天数；

（3）求该城市某一周至少有 2天的空气质量为良或轻微污染的概率.

(结果用分数表示．已知 $5^7=78125,2^7=128,\frac{3}{1825}+\frac{2}{365}+\frac{7}{1825}+\frac{3}{1825}+\frac{8}{9125}=\frac{123}{9125},365=73\times 5$ ）

已知向量 $a=(\mathit{sin}\theta ,-2)与b=(1,\mathit{cos}\theta )$互相垂直，其中 $\theta \in (0,\frac{\pi }{2})$．

（1）求 $\mathit{sin}\theta 和\mathit{cos}\theta$的值；

（2）若 $\mathit{sin}(\theta -\phi )=\frac{\sqrt{10}}{10},0<\phi <\frac{\pi }{2}$，求 $\mathit{cos}\phi$的值．     

已知抛物线 $C：x^2=2\mathit{py}(p>0)$ 上一点 $A(m,4)$ 到其焦点的距离为 $\frac{17}{4}$ .

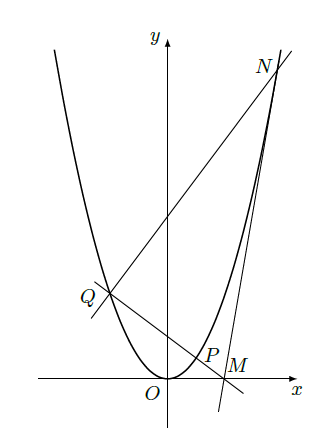
（Ⅰ）求 p于 m的值；

（Ⅱ）设抛物线C上一点 p的横坐标为 t（ t>0）,过 p的直线交C于另一点 Q，交 x轴于 M点，过点 Q作 PQ的垂线交 C于另一点 N.若 MN是 C的切线，求 t的最小值;

已知函数 $f\left(x\right)=x^3+\left(1-a\right)x^2-a\left(a+2\right)x+b(a,b\in R)$.

（Ⅰ）若函数 $f\left(x\right)$的图像过原点，且在原点处的切线斜率是-3，求a，b的值；

（Ⅱ）若函数 $f\left(x\right)$在区间 $\left(-1,1\right)$上不单调，求a的取值范围.       

设 $S_n$ 为数列 $\left\{a_n\right\}$ 的前 n项和， $S_n=\text{k}{\text{n}}^2+n,n\in N^{*}$ ，其中 $k$ 是常数.

（Ⅰ）求 $a_1$ 及 $a_n$ ；

（Ⅱ）若对于任意的 $m\in N^{*}$ , $a_m$ , $a_{2m}$ , $a_{4m}$ 成等比数列，求 k的值.

如图， $\mathit{DC}\perp \mathit{平面}\mathit{ABC}$ , $\mathit{EB}\parallel \mathit{DC}$ , $\mathit{AC}=\mathit{BC}=\mathit{EB}=2\mathit{DC}=2$ , $\angle \mathit{ACB}=120°$ ，P,Q分别为AE,AB的中点.

（Ⅰ）证明： $\mathit{PQ}\parallel \mathit{平面}\mathit{ACD}$ ；

（Ⅱ）求 $\mathit{AD}$ 与 $\mathit{平面}\mathit{ABE}$ 所成角的正弦值.

在 $\mathit{\Delta ABC}$ 中，角A,B,C所对的边分别为a,b,c,且满足 $\mathit{cos}\frac{A}{2}=\frac{2\sqrt{5}}{5}$ ， $\overrightarrow{\mathit{AB}}\cdot \overrightarrow{\mathit{AC}}=3$ .

(Ⅰ)求 $△\mathit{ABC}$ 的面积；     

（Ⅱ）若 $c=1$ ，求 $a$ 的值.

双曲线 $C_1:\frac{x^2}{4^2}-\frac{y^2}{b^2}=1$ ，圆 $C_2:x^2+y^2=4+b^2(b>0)$ 在第一象限交点为A， $A(x_A,y_A)$ ，曲线 $\Gamma \left\{\begin{array}{c}\frac{x^2}{4}-\frac{y^2}{b^2}=1,\left|x\right|>x_A\\ x^2+y^2=4+b^2,\left|x\right|>x_A\end{array}\right.$ 。

（1）若 $x_A=\sqrt{6}$ ，求b；

（2）若 $b=\sqrt{5}$ ， $C_2$ 与x轴交点记为 $F_1、F_2$ ，P是曲线 $\Gamma$ 上一点，且在第一象限，并满足 $\left|P{F}_1\right|=8$ ，求∠ $F_{1}P{F}_2$ ；

（3）过点 $S(0,2+\frac{b^2}{2})$ 且斜率为 $-\frac{b}{2}$ 的直线 $l$ 交曲线 $\Gamma$ 于M、N两点，用b的代数式表示 $\overrightarrow{\mathit{OM}}\bullet \overrightarrow{\mathit{ON}}$ ，并求出 $\overrightarrow{\mathit{OM}}\bullet \overrightarrow{\mathit{ON}}$ 的取值范围。

已知： $\nu =\frac{q}{x}$， $x\in (0,80]$，且 $\nu =\left\{\begin{array}{c}100\text{-135}(\frac{1}{3}{)}^{\frac{80}{x}},x\in (0,40)\\ -k(x-40)+85,x\in [40,80]\end{array}\right.(k>0)$，

（1）若v>95，求x的取值范围；

（2）已知x=80时，v=50，求x为多少时，q可以取得最大值，并求出该最大值。

已知 $f\left(x\right)\text{=sin}\mathit{\omega x}(\omega >0)$.

（1）若f(x)的周期是4π，求 $\omega$，并求此时 $f\left(x\right)=\frac{1}{2}$的解集；

（2）已知 $\omega =1$， $g\left(x\right)=f^2\left(x\right)+\sqrt{3}f(-x)f(\frac{\pi }{2}-x)$， $x\in \left[0,\frac{\pi }{4}\right]$，求g(x)的值域.

已知边长为1的正方形ABCD，沿BC旋转一周得到圆柱体。

（1）求圆柱体的表面积；

（2）正方形ABCD绕BC逆时针旋转 $\frac{\pi }{2}$ 到 $A_1\mathit{BC}{D}_1$ ，求 $A{D}_1$ 与平面ABCD所成的角。

已知数集 $A=\{a_1,a_2,\cdots a_n\}(1\le a_1<a_2<\cdots a_n,n\ge 2)$ 具有性质 $P$ ；对任意的 $i,j(1\le i\le j\le n)$ ， $a_i{a}_j$ 与 $\frac{a_j}{a_i}$ 两数中至少有一个属于 $A$ 。

（Ⅰ）分别判断数集 $\{1,3,4\}$ 与 $\{1,2,3,6\}$ 是否具有性质 $P$ ，并说明理由；

（Ⅱ）证明： $a_1=1$ ，且 $\frac{a_1+a_2+\cdots +a_n}{a_1^{-1}+a_2^{-1}+\cdots +a_n^{-1}}=a_n;$

（Ⅲ）证明：当 $n=5$ 时， $a_1{a}_2{a}_3{a}_4{a}_5$ 成等比数列。