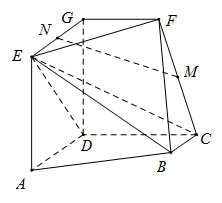
如图, 且AD=2BC, , 且EG=AD, 且CD=2FG, ,DA=DC=DG=2.
(Ⅰ)若M为CF的中点,N为EG的中点,求证: ;
(Ⅱ)求二面角 的正弦值;
(Ⅲ)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.
已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
在 中,内角 A, B, C所对的边分别为 a, b, c.已知 .
(1)求角 B的大小;
(2)设 a=2, c=3,求 b和 的值.
在直角坐标系 中,曲线 的方程为 .以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
(1)求 的直角坐标方程;
(2)若 与 有且仅有三个公共点,求 的方程.
某工厂的某种产品成箱包装,每箱 件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取 件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为 ,且各件产品是否为不合格品相互独立.
(1)记 件产品中恰有 件不合格品的概率为 ,求 的最大值点 ;
(2)现对一箱产品检验了 件,结果恰有 件不合格品,以(1)中确定的 作为 的值.已知每件产品的检验费用为 元,若有不合格品进入用户手中,则工厂要对每件不合格品支付 元的赔偿费用.
(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为 ,求 ;
(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
设椭圆 的右焦点为 ,过 的直线 与 交于 两点,点 的坐标为 .
(1)当 与 轴垂直时,求直线 的方程;
(2)设 为坐标原点,证明: .
如图,四边形
为正方形,
分别为
的中点,以
为折痕把  折起,使点
到达点
的位置,且
.
折起,使点
到达点
的位置,且
.
(1)证明:平面 平面 ;
(2)求 与平面 所成角的正弦值.

在直角坐标系 中,曲线 的参数方程为 ( 为参数),直线 的参数方程为 ( 为参数).
(1)求 和 的直角坐标方程;
(2)若曲线 截直线 所得线段的中点坐标为 ,求 的斜率.
如图,在三棱锥 中, , , 为 的中点.

(1)证明: 平面 ;
(2)若点 在棱 上,且二面角 为 ,求 与平面 所成角的正弦值.
试题篮
()