(本小题满分12分)已知双曲线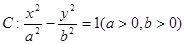 , 若双曲线的渐近线过点
, 若双曲线的渐近线过点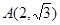 , 且双曲线过点
, 且双曲线过点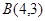
(1)求双曲线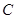 的方程;
的方程;
(2)若双曲线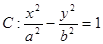 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 在
在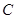 上且直线
上且直线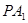 的斜率的取值范围是
的斜率的取值范围是 ,求直线
,求直线 斜率的取值范围.
斜率的取值范围.
(本小题满分10分)如图甲,⊙ 的直径
的直径 ,圆上两点
,圆上两点 在直径
在直径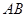 的两侧,使
的两侧,使 ,
,  .沿直径
.沿直径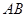 折起,使两个半圆所在的平面互相垂直(如图乙),
折起,使两个半圆所在的平面互相垂直(如图乙),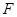 为
为 的中点.根据图乙解答下列各题:
的中点.根据图乙解答下列各题:
(1)求点 到
到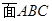 的距离;
的距离;
(2)在 弧上是否存在一点
弧上是否存在一点 ,使得
,使得 ∥平面
∥平面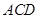 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
在数列 中,
中, ,
, ,
, ,其中
,其中 .
.
(1)求证:数列 为等差数列;
为等差数列;
(2)设 ,试问数列
,试问数列 中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出这三项;若不存在,说明理由.
(3)已知当 且
且 时,
时, ,其中
,其中 ,
, ,
, ,
, ,求满足等式
,求满足等式 的所有
的所有 的值.
的值.
(本小题12分)己知 、
、 、
、 是椭圆
是椭圆 :
: (
( )上的三点,其中点
)上的三点,其中点 的坐标为
的坐标为 ,
, 过椭圆的中心,且
过椭圆的中心,且 ,
, 。
。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 的直线
的直线 (斜率存在时)与椭圆
(斜率存在时)与椭圆 交于两点
交于两点 ,
, ,设
,设 为椭圆
为椭圆 与
与 轴负半轴的交点,且
轴负半轴的交点,且 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分15分)
设抛物线 :
:
 的焦点为
的焦点为 ,过
,过 且斜率为
且斜率为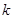 的直线
的直线 交抛物线
交抛物线 于
于 ,
, 两
两
点,且 .
.
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ)已知点 ,且
,且 的面积为
的面积为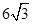 ,求
,求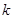 的值.
的值.
(本小题满分14分)已知函数f(x)=xln(1+x)-a(x+1),其中a为实常数.
(1)当x∈[1,+∞)时,f′(x)>0恒成立,求a的取值范围;
(2)求函数g(x)=f′(x)- 的单调区间.
的单调区间.
数列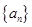 的首项为
的首项为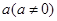 ,前n项和为
,前n项和为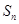 ,且
,且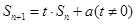 ,设
,设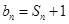 ,cn=k+b1+b2+…+bn(k∈R+).
,cn=k+b1+b2+…+bn(k∈R+).
(1)求数列{an}的通项公式;
(2)当t=1时,若对任意n∈N*,|bn|≥|b3|恒成立,求a的取值范围;
(3)当t≠1时,试求三个正数a,t,k的一组值,使得{cn}为等比数列,且a,t,k成等差数列.
已知椭圆C1的方程为 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点。
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点。
(1)求双曲线C2的方程;
(2)若直线l: 与双曲线C2恒有两个不同的交点A和B,且
与双曲线C2恒有两个不同的交点A和B,且 (其中O为原点),求k的取值范围。
(其中O为原点),求k的取值范围。
已知F1、F2分别是椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)若P是第一象限内该图形上的一点, ,求点P的坐标;
,求点P的坐标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于同的两点A、B,且∠AOB为锐角(其中O为作标原点),求直线 的斜率
的斜率 的取值范围.
的取值范围.
)在平面直角坐标系xOy中,点P(a,b)(a>b>0)为动点,F1、F2分别为椭圆 =1的左、右焦点.已知△F1PF2为等腰三角形.
=1的左、右焦点.已知△F1PF2为等腰三角形.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点,M是直线PF2上的点,满足 =-2,求点M的轨迹方程.
=-2,求点M的轨迹方程.
某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段 ,
, …
… 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是40~50分及90~100分的学生中选两人,记他们的成绩为x,y,求满足“ ”的概率.
”的概率.
试题篮
()