高中物理等势面试题

如图所示，水平放置的平行板电容器，上板带负电，下板带正电，断开电源，带电小球以速度v₀水平射入电场，且沿下板边缘飞出．若下板不动，将上板上移一小段距离，小球仍以相同的速度v₀从原处飞入，则带电小球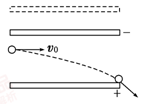

A．仍沿原轨迹由下板边缘飞出

B．将打在下板中央

C．不发生偏转，沿直线运动

D．若上板不动，将下板上移一段距离，小球可能打在下板的中央

如图中虚线为匀强电场中与场强方向垂直的等间距平行直线，两粒子M、N质量相等，所带电荷的绝对值也相等．现将M、N从虚线上的O点以相同速率射出，两粒子在电场中运动的轨迹分别如图中两条实线所示．点a.b.c为实线与虚线的交点，已知O点电势高于c点电势．若不计重力，则(       )

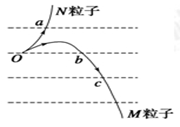
A．M带负电荷，N带正电荷

B．N在a点的速度与M在c点的速度大小相同

C．N在从O点运动至a点的过程中克服电场力做功

D．M在从O点运动至b点的过程中，电场力对它做的功等于零

一个电子以v₀＝4×10⁷m/s的速度，方向与电场方向相同，射入电场强度E＝2×10⁵V/m的匀强电场中，如图所示，已知电子电量e＝－1.6×10^－19C，电子质量m＝9.1×10^－31kg.试求：

（1）从电子的入射点到达速度为0之点的两点间电势差是多少? 两点间距离是多少?
（2）电子到达速度为0之前所需的时间是多少?

两平行金属板长为L，板间距离为d，从两板左端正中间有带电粒子持续飞入，如图所示。粒子的电量为q，质量为m，初速度方向平行于极板，大小为v₀，在两极板上加一恒定电压U，不计带电粒子重力作用。求：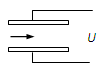

（1）带电粒子如果能从金属板右侧飞出，粒子在电场中运动的时间是多少？
（2）粒子能从右侧飞出，粒子在电场中的加速度是多少？
（3）如粒子恰好能从右侧极板边缘飞出，求恒定电压U，金属板长L，板间距离d，粒子的电量q，质量m，初速度大小v₀之间的数量关系，

如图所示，A是一个质量为kg表面绝缘的薄板，薄板静止在光滑的水平面上，在薄板左端放置一质量为kg带电量为C的绝缘物块，在薄板上方有一水平电场，可以通过外接装置控制其大小及方向.接通装置先产生一个方向水平向右，大小V/m的电场，薄板和物块开始运动，作用时间2s后，改变电场，电场大小变为V/m，方向向左，电场作用一段时间后，关闭电场，薄板正好到达目的地，且薄板和物块的速度都恰好为零. 已知薄板与物块间的动摩擦因数=0.1，（薄板不带电，物块体积大小不计，g取10m/s²）求：

（1）在电场E₁作用下物块和薄板的加速度各为多大；
（2）电场E₂作用的时间；
（3）从薄板和物块开始运动到薄板和物块的速度恰好为零过程中电场力做功为多少。

如图所示，一带电平行板电容器与水平方向成37°放置，下方有绝缘挡板支撑，板间距d=2.88cm，一带正电的小球的质量为0.02g，电荷量为10^﹣7C，由电容器的中心A点静止释放恰好沿水平直线AB向右运动，从上极板边缘飞出进入边界BC右侧的水平向左的匀强电场区域，场强为2×l0³V/m，经过一段时间后发现小球打在竖直挡板C点正下方的D处，（取g=10m/s²）求：

（1）平行板电容器内的场强大小
（2）小球从上极板边缘飞出的速度
（3）CD间的距离．

平行板电容器内部有匀强电场，一束离子从两板正中P处垂直电场入射，出现如图所示的偏转轨迹，则

A．若为同种离子，射入电场的初速度最大

B．若为同种离子，射入电场的初速度最大

C．若初速度相同，在电场中的加速度最大

D．若初速度相同，在电场中的加速度最大

如图所示，匀强电场中有a、b、c三点，ab=5cm，bc=12cm，其中ab沿电场方向，bc和电场方向成60°角，一个电量为q=4×10^-8C 的正电荷从a移到b电场力做功为W₁=1.2×10^-7J。
则：

（1）匀强电场的场强E；（2）电荷从b移到c，电场力做功W₂；（3）a、c两点的电势差U_ac；

如图所示，在直角坐标系xoy的第一象限中，存在竖直向下的匀强电场，电场强度大小为，虚线是电场的理想边界线，虚线右端与x轴的交点为A，A点坐标为（L，0），虚线与x轴所围成的空间内没有电场；在第二象限存在水平向右的匀强电场，电场强度大小为，M（-L，L）和N（-L，0）两点的连线上有一个产生粒子的发生器装置，不断产生质量均为m，电荷量均为q的带正电的静止粒子，不计粒子的重力和粒子之间的相互作用力，且整个装置处于真空中，

（1）若粒子从M点由静止开始运动，进入第一象限后始终在电场中运动并恰好到达A点，求这个过程中该粒子运动的时间及到达A点的速度大小；
（2）若从MN线上M点下方由静止发出的所有粒子，在第二象限的电场加速后，经第一象限的电场偏转穿过虚线边界后都能到达A点，求此边界（图中虚线）方程

如图所示，AB是一倾角为θ=37°的绝缘粗糙直轨道，滑块与斜面间的动摩擦因数μ=0.30，BCD是半径为R=0.2m的光滑圆弧轨道，它们相切于B点，C为圆弧轨道的最低点，整个空间存在着竖直向上的匀强电场，场强E=4.0×10³N/C，质量m=0.20kg的带电滑块从斜面顶端由静止开始滑下。已知斜面AB对应的高度h=0.24m，滑块带电荷q=-5.0×10^-4 C，取重力加速度g=10m/s2，sin37°=0.60，cos37°=0.80。求：

（1）滑块从斜面最高点滑到斜面底端B点时的速度大小；
（2）滑块滑到圆弧轨道最低点C时对轨道的压力。

如图所示为一真空示波管，电子从灯丝K发出（初速度不计），经灯丝与A板间的加速电压U₁加速，从A板中心孔沿中心线KO射出，然后进入两块平行金属板M、N形成的偏转电场中（偏转电场可视为匀强电场），电子进入M、N间电场时的速度与电场方向垂直，电子经过电场后打在荧光屏上的P点．已知加速电压为U₁，M、N两板间的电压为U₂，两板间的距离为d，板长为L₁，板右端到荧光屏的距离为L₂，电子的质量为m，电荷量为e．求：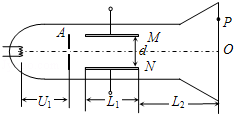

（1）电子穿过A板时的速度大小；
（2）电子从偏转电场射出时的侧移量；
（3）P点到O点的距离．

如图所示，在xOy平面的第一象限内，分布有沿x轴负方向的场强E=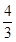×10⁴N/C的匀强电场，第四象限内分布有垂直纸面向里的磁感应强度B₁="0.2" T的匀强磁场，第二、三象限内分布有垂直纸面向里的磁感应强度B₂的匀强磁场。在x轴上有一个垂直于y轴的平板OM，平板上开有一个小孔P，P处连接有一段长度d=lcm内径不计的准直管，管内由于静电屏蔽没有电场。y轴负方向上距O点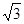cm的粒子源S可以向第四象限平面内各个方向发射a粒子，假设发射的a粒子速度大小v均为2×10⁵m/s，此时有粒子通过准直管进入电场, 打到平板和准直管管壁上的a粒子均被吸收。已知a粒子带正电，比荷为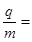5×l0⁷C/kg，重力不计，求：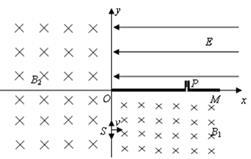

（1）a粒子在第四象限的磁场中运动时的轨道半径和粒子从S到达P孔的时间；
（2）除了通过准直管的a粒子外，为使其余a粒子都不能进入电场，平板OM的长度至少是多长？
（3）经过准直管进入电场中运动的a粒子，第一次到达y轴的位置与O点的距离；
（4）要使离开电场的a粒子能回到粒子源S处，磁感应强度B₂应为多大？

如图所示，质量为m，电荷量为e的电子，从A点以速度v₀垂直于电场方向射入一个电场强度为E的匀强电场中，从B点射出电场时的速度方向与电场线成120°角，电子重力不计。求：

(1)电子在电场中的加速度大小a及电子在B点的速度大小v_B；
(2)A、B两点间的电势差U_AB；
(3)电子从A运动到B的时间t_AB。

虚线MN下方有竖直向上的匀强电场，场强大小E=2×10³V/m，MN上方有一竖直长为L=0.5m的轻质绝缘杆，杆的上下两端分别固定一带电小球A、B（可看成质点），质量均为m=0.01kg，A带电量为；B带电量，B到MN的距离h=0.05m。现将杆由静止释放（g取10m/s²），求：

（1）小球B在匀强电场中，而A还未进入电场时，两小球的加速度大小。
（2）从开始运动到A刚要进入匀强电场过程的时间。

在电场中一条电场线上有A.B两点，如图所示.若将一负电荷q=2.0×10^-7C，从A点移至B点，电荷克服电场力做功4.0×10^-4J.试求：

(1)A.B两点的电势差U_ab多大?哪一点电势高?
(2)在这一过程中，电荷的电势能怎样变化?
(3)如在这一电场中有另一点C，已知U_AC=500V，若把这一负荷从B移至C电场力做多少功?是正功还是负功?