高中物理等势面试题

如图所示，当K₁、K₂均闭合时，一质量为m、带电荷量为q的液滴，静止在电容器的两平行金属板A.B间，现保持K₁闭合，将K₂断开，然后将B板向下平移一段距离，则下列说法正确的是（   ）


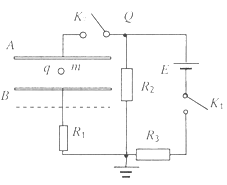
A．电容器的电容变小
B．A板的电势比电路中Q点的电势高
C．液滴向下加速运动
D．液滴的电势能减小

两异种点电荷电场中的部分等势面如图所示，已知A点电势高于B点电势｡若位于a、b处点电荷的电荷量大小分别为q_a和q_b，则

A．ａ处为正电荷，qa＜qb

B．ａ处为正电荷，qa＞qb

C．ａ处为负电荷，qa＜qb

D．ａ处为负电荷，qa＞qb

带有等量异号电荷、相距10cm的平行板A和B之间有一个匀强电场,如图所示,电场强度E=2×10⁴V/m,方向向下。电场中C点距B板3cm,D点距A板2cm.

(1)如果令B板接地(即B板电势为零),则C点和D点的电势各是多少？
(2)C,D两点U_CD等于多少？
(3)一个电子从C点移动到D点,静电力做多少功？ 如果使电子先移到P点,再移到D点,静电力做的功是否发生变化？（e=-1.6×10^-19C）

一带电粒子在电场中仅受静电力作用，做初速度为零的直线运动，取该直线为轴，起始点为坐标原点，其电势能与位移的关系如图所示，下列图象中合理的是（）

A．	粒子所处位置电势与位移关系	B．	粒子动能与位移关系
C．	粒子速度与位移关系	D．	粒子加速度与位移关系

一带电油滴在匀强电场E中的运动轨迹如图中虚线所示，电场方向竖直向下。若不计空气阻力，则此带电油滴从a运动到b的过程中，能量变化情况为 (  )

A．动能减小

B．电势能增加

C．动能和电势能之和减小

D．重力势能和电势能之和增加

如图甲所示，MN为很大的薄金属板（可理解为无限大），金属板原来不带电．在金属板的右侧，距金属板距离为d的位置上放入一个带正电、电荷量为q的点电荷，由于静电感应产生了如图甲所示的电场分布．P是点电荷右侧，与点电荷之间的距离也为d的一个点，几位同学想求出P点的电场强度大小，但发现问题很难．他们经过仔细研究，从图乙所示的电场得到了一些启示，经过查阅资料他们知道：图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的．图乙中两异号点电荷量的大小均为q，它们之间的距离为2d，虚线是两点电荷连线的中垂线．由此他们分别求出了P点的电场强度大小，一共有以下四个不同的答案（k为静电力常量），其中正确的是

A．

B．

C．

D．

在电场中，把电荷量为4×10^﹣9C的正电荷从A点移到B点，克服电场力做功8×10^﹣8J，以下说法中正确的是（）

A．正电荷在B点具有的电势能是8×10^﹣8 J

B．B点的电势是20 V

C．正电荷的电势能增加了8×l0^﹣8J

D．正电荷的电势能减少了8×10^﹣8J

a、b、c、d分别是一个菱形的四个顶点，abc=120º．现将三个等量的正点电荷+Q分别固定在a、b、c三个顶点上，则下列判断正确的是

A．d点电场强度的方向由d指向O

B．O点处的电场强度是d点处的电场强度的2倍

C．bd连线为一等势线

D．引入一个电量为+q的点电荷，依次置于O点和d点，

则在d点所具有的电势能大于在O点所具有的电势能

如图所示，水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场，电场强度E=1.0×10⁴N/C。现有一电荷量q=+1.0×10^-4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体运动到圆形轨道最低点B时的速度v_B=5.0m/s。已知带电体与水平轨道间的动摩擦因数μ=0.50，重力加速度g=l0m/s²。求

（1）带电体在水平轨道上的释放点P到B点的距离；
（2）带电体第一次经过C点时的速度。

如图所示为一真空示波管，电子从灯丝K发出（初速度不计），经灯丝与A板间的加速电压U₁加速，从A板中心孔沿中心线KO射出，然后进入两块平行金属板M、N形成的偏转电场中（偏转电场可视为匀强电场），电子进入M、N间电场时的速度与电场方向垂直，电子经过电场后打在荧光屏上的P点．已知加速电压为U₁，M、N两板间的电压为U₂，两板间的距离为d，板长为L₁，板右端到荧光屏的距离为L₂，电子的质量为m，电荷量为e．求：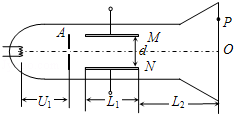

（1）电子穿过A板时的速度大小；
（2）电子从偏转电场射出时的侧移量；
（3）P点到O点的距离．

如图所示，在xOy平面的第一象限内，分布有沿x轴负方向的场强E=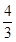×10⁴N/C的匀强电场，第四象限内分布有垂直纸面向里的磁感应强度B₁="0.2" T的匀强磁场，第二、三象限内分布有垂直纸面向里的磁感应强度B₂的匀强磁场。在x轴上有一个垂直于y轴的平板OM，平板上开有一个小孔P，P处连接有一段长度d=lcm内径不计的准直管，管内由于静电屏蔽没有电场。y轴负方向上距O点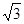cm的粒子源S可以向第四象限平面内各个方向发射a粒子，假设发射的a粒子速度大小v均为2×10⁵m/s，此时有粒子通过准直管进入电场, 打到平板和准直管管壁上的a粒子均被吸收。已知a粒子带正电，比荷为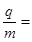5×l0⁷C/kg，重力不计，求：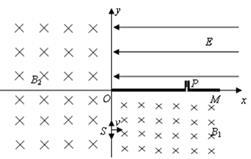

（1）a粒子在第四象限的磁场中运动时的轨道半径和粒子从S到达P孔的时间；
（2）除了通过准直管的a粒子外，为使其余a粒子都不能进入电场，平板OM的长度至少是多长？
（3）经过准直管进入电场中运动的a粒子，第一次到达y轴的位置与O点的距离；
（4）要使离开电场的a粒子能回到粒子源S处，磁感应强度B₂应为多大？

如图所示，质量为m，电荷量为e的电子，从A点以速度v₀垂直于电场方向射入一个电场强度为E的匀强电场中，从B点射出电场时的速度方向与电场线成120°角，电子重力不计。求：

(1)电子在电场中的加速度大小a及电子在B点的速度大小v_B；
(2)A、B两点间的电势差U_AB；
(3)电子从A运动到B的时间t_AB。

虚线MN下方有竖直向上的匀强电场，场强大小E=2×10³V/m，MN上方有一竖直长为L=0.5m的轻质绝缘杆，杆的上下两端分别固定一带电小球A、B（可看成质点），质量均为m=0.01kg，A带电量为；B带电量，B到MN的距离h=0.05m。现将杆由静止释放（g取10m/s²），求：

（1）小球B在匀强电场中，而A还未进入电场时，两小球的加速度大小。
（2）从开始运动到A刚要进入匀强电场过程的时间。

如图所示，在xOy坐标系中，两平行金属板如图放置，OD与x轴重合，板的左端与原点O重合，板长L=2m，板间距离d=1m，紧靠极板右侧有一荧光屏。两金属板间电压U_AO变化规律如图所示，变化周期为T=2×10^-3s，U₀=10³V，t=0时刻一带正电的粒子从左上角A点，以平行于AB边v₀=1000m/s的速度射入板间，粒子电量q=1×10^-5C，质量m=1×10^-7kg。不计粒子所受重力。求：

（1）粒子在板间运动的时间；
（2）粒子打到荧光屏上的纵坐标；
（3）粒子打到屏上的动能。

“电子能量分析器”主要由处于真空中的电子偏转器和探测板组成．偏转器是由两个相互绝缘、半径分别为R_A和R_B的同心金属半球面A和B构成，A、B为电势值不等的等势面，其过球心的截面如图所示．一束电荷量为E、质量为m的电子以不同的动能从偏转器左端M的正中间小孔垂直入射，进入偏转电场区域，最后到达偏转器右端的探测板N，其中动能为E_k0的电子沿等势面C做匀速圆周运动到达N板的正中间．忽略电场的边缘效应．

（1）判断球面A、B的电势高低，并说明理由；
（2）求等势面C所在处电场强度E的大小；
（3）若半球面A、B和等势面C的电势分别为φ_A、φ_B和φ_C，则到达N板左、右边缘处的电子，经过偏转电场前、后的动能改变量△E_k左和△E_k右分别为多少？
（4）比较|△E_k左|和|△E_k右|的大小，并说明理由．