如图是过山车的部分模型图。模型图中光滑圆形轨道的半径R=8.1m,该光滑圆形轨道固定在倾角为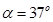 斜轨道面上的Q点,圆形轨道的最高点A与P点平齐,圆形轨道与斜轨道之间圆滑连接。现使小车(视作质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为
斜轨道面上的Q点,圆形轨道的最高点A与P点平齐,圆形轨道与斜轨道之间圆滑连接。现使小车(视作质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为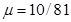 ,不计空气阻力,过山车质量为20kg,取g=10m/s2,
,不计空气阻力,过山车质量为20kg,取g=10m/s2,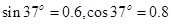 。若小车恰好能通过圆形轨道的最高点A处,求:
。若小车恰好能通过圆形轨道的最高点A处,求: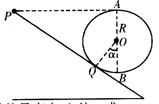
(1)小车在A点的速度为多大;
(2)小车在圆形轨道的最低点B时对轨道的压力为重力的多少倍;
(3)小车在P点的动能.
如图甲所示,放在光滑水平地面上的长木板质量M="0" 5kg,木板右端放一质量m="0" 5kg的滑块(可视为质点),滑块与木板间的动摩擦因数 ="0" 4;滑块的正上方有一悬点O,通过长l="0" 8m的轻绳吊一质量m0="1" 0kg的小球 现将小球拉至与O点处于同一水平位置,由静止释放,小球摆至最低点时与滑块发生正碰,且m0与m只碰一次,小球碰后的动能与其向上摆动高度的关系如图乙所示,g取10m/s2,求:
="0" 4;滑块的正上方有一悬点O,通过长l="0" 8m的轻绳吊一质量m0="1" 0kg的小球 现将小球拉至与O点处于同一水平位置,由静止释放,小球摆至最低点时与滑块发生正碰,且m0与m只碰一次,小球碰后的动能与其向上摆动高度的关系如图乙所示,g取10m/s2,求:
(1)碰前瞬间绳子对小球拉力的大小;
(2)碰后瞬间滑块速度的大小;
(3)要使滑块不会从木板上滑下,则木板的长度应滿足什么条件?
“超级地球”是指围绕恒星公转的类地行星 科学家们发现有两颗未知质量的不同“超级地球”环绕同一颗恒星公转,周期分别为10天和20天 根据上述信息可以计算两颗“超级地球”( )
A 质量之比
B 所受的引力之比
C 角速度之比
D 向心加速度之比
研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时。假设这种趋势会持续下去,而地球的质量保持不变,未来人类发射的地球同步卫星与现在的相比
| A.线速度变小 | B.角速度变大 |
| C.向心加速度变大 | D.距地面的高度变小 |
如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l,水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态。可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回。已知R=0.4 m,l=2.5 m,v0=6 m/s,物块质量m=1 kg,与PQ段间的动摩擦因数μ=0.4,轨道其它部分摩擦不计。取g=10 m/s2。求: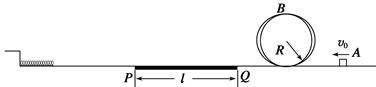
(1)物块经过圆轨道最高点B时对轨道的压力;
(2)物块从Q运动到P的时间及弹簧获得的最大弹性势能;
(3)物块仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动。
如图所示,光滑的水平面AB与半径R=0.4m的光滑竖直半圆轨道BCD在B点相切,D点为半圆轨道最高点,A点的右侧连接一粗糙的水平面。用细线连接甲、乙两物体,中问夹一轻质压缩弹簧,弹簧与甲、乙两物体不拴接,甲的质量朋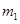 =4kg,乙的质量
=4kg,乙的质量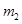 =5kg,甲、乙均静止。若固定乙,烧断细线,甲离开弹簧后经过B点进入半圆轨道,过D点时对轨道的压力恰好为零。取g=10m/s2,甲、乙两物体均可看作质点,求:
=5kg,甲、乙均静止。若固定乙,烧断细线,甲离开弹簧后经过B点进入半圆轨道,过D点时对轨道的压力恰好为零。取g=10m/s2,甲、乙两物体均可看作质点,求: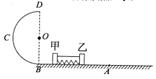
(1)甲离开弹簧后经过B点时的速度的大小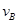 ;
;
(2)在弹簧压缩量相同的情况下,若固定甲,烧断细线,乙物体离开弹簧后从A点进入动摩擦因数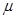 =0.4的粗糙水平面,则乙物体在粗糙水平面运动的位移S。
=0.4的粗糙水平面,则乙物体在粗糙水平面运动的位移S。
如下图所示,长为l的细绳一端固定在O点,另一端拴住一个小球,在O点的正下方与O点相距 的地方有一枚与竖直平面垂直的钉子;把小球拉起使细绳在水平方向伸直,由静止开始释放,当细绳碰到钉子的瞬间,下列说法正确的是( )
的地方有一枚与竖直平面垂直的钉子;把小球拉起使细绳在水平方向伸直,由静止开始释放,当细绳碰到钉子的瞬间,下列说法正确的是( )
| A.小球的线速度不发生突变 |
| B.小球的角速度突然增大到原来的2倍 |
| C.小球的向心加速度突然增大到原来的2倍 |
| D.绳子对小球的拉力突然增大到原来的2倍 |
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的:( )
| A.运动周期相同 | B.运动线速度相同 |
| C.运动角速度相同 | D.向心加速度相同 |
同学们参照伽利略时期演示平抛运动的方法制作了如图所示的实验装置。图中水平放置的底板上竖直地固定有板和
板。
板上部有一半径为
的
圆弧形的粗糙轨道,
为最高点,
为最低点,
点处的切线水平,距底板高为
.
板上固定有三个圆环.将质量为
的小球从
处静止释放,小球运动至
飞出后无阻碍地通过各圆环中心,落到底板上距
水平距离为
处。不考虑空气阻力,重力加速度为
.求:

(1)距水平距离为
的圆环中心到底板的高度.
(2)小球运动到点时速度的大小以及对轨道压力的大小和方向;
(3)摩擦力对小球做的功
如图所示,一半径为,粗糙程度处处相同的半圆形轨道竖直固定放置,直径
水平。一质量为
的质点自
点上方高度
处由静止开始下落,恰好从
点进入轨道。质点滑到轨道最低点
时,对轨道的压力为
,
为重力加速度的大小。用
表示质点从
点运动到
点的过程中客服摩擦力所做的功。则()

| A. |
 ,质点恰好可以到达 ,质点恰好可以到达
|
| B. |
 ,质点不能到达 ,质点不能到达
|
| C. |
 ,质点到达 ,质点到达
|
| D. |
 ,质点到达 ,质点到达
|
某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=60kg的参赛者(可视为质点),在河岸上A点双手紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=5.0m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内,若参赛者双手抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内。(sin37°=0.6,cos37°=0.8, g=10m/s2)
(1)求参赛者经过B点时速度的大小v;
(2)求参赛者从台阶上A点跃出时的动能EK;
(3)若手与绳之间的动摩擦因数为0.6,参赛者要顺利完成比赛,则每只手对绳的最大握力不得小于多少?(设最大静摩擦等于滑动摩擦力)
如图所示为通过弹射器研究轻弹簧的弹性势能的实验装置。半径为R的光滑3/4圆形轨道竖直固定于光滑水平面上并与水平地面相切于B点,弹射器固定于A处。某次实验过程中弹射器射出一质量为m的小球,恰能沿圆轨道内侧到达最髙点C,然后从轨道D处(D与圆心等高)下落至水平面。忽略空气阻力,取重力加速度为g。下列说法正确的是( )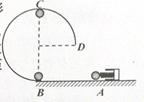
A.小球从D处下落至水平面的时间小于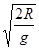 |
| B.小球运动至最低点B时对轨道压力为5mg |
| C.小球落至水平面时的动能为2mgR |
D.释放小球前弹射器的弹性势能为 |
如图所示,一内壁光滑、质量为m、半径为 r的环形细圆管,用硬杆竖直固定在天花板上。有一质量为 m 的小球(可看作质点)在圆管中运动。小球以速率v0经过圆管最低点时,杆对圆管的作用力大小为( )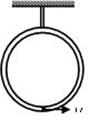
A. |
B. |
C.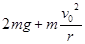 |
D. |
如图所示,用一根长为l=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为T。求(取g=10m/s2,结果可用根式表示):
(1)若要小球离开锥面,则小球的角速度ω0至少为多大?
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω'为多大?
(3)细线的张力T与小球匀速转动的加速度ω有关,请在坐标纸上画出ω的取值范围在0到ω'之间时的T—ω2的图象(要求标明关键点的坐标值)。
如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l,水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态。可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回。已知R=0.4 m,l=2.5 m,v0=6 m/s,物块质量m=1 kg,与PQ段间的动摩擦因数μ=0.4,轨道其它部分摩擦不计。取g=10 m/s2。求:
(1)物块经过圆轨道最高点B时对轨道的压力;
(2)物块从Q运动到P的时间及弹簧获得的最大弹性势能;
(3)物块仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动。
试题篮
()