高中物理探究向心力大小与半径、角速度、质量的关系计算题

一根长为l的丝线吊着一质量为m，带电荷量为q的小球静止在水平向右的匀强电场中，如图所示，丝线与竖直方向成37°角，现突然将该电场方向变为向下且大小不变，不考虑因电场的改变而带来的其他影响(重力加速度为g)，求：

(1)匀强电场的电场强度的大小；(sin37°＝0.6，cos37°＝0.8)，
(2)小球经过最低点对丝线的拉力．

如图所示，半径为R的1/4光滑圆弧轨道与光滑水平面相切于B点，O为光滑圆弧的圆心，其中OB竖直，OC水平，且AB=R，整个空间存在水平向右的匀强电场，质量为m的带正电小球从A点静止释放，其所受电场力为重力的3/4倍，重力加速度为g，求：

（1）小球到达C点时对轨道的压力大小；
（2）小球从A点运动到C点过程中最大速度的大小．

(15分)在半径R=4000km的某星球表面，宇航员做了如下实验，实验装置如图甲所示，竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成，将质量m=0.2kg的小球从轨道上高H处的某点由静止滑下，用力传感器测出小球经过C点时对轨道的压力F，改变H的大小，可测出相应的F大小，F随H的变化关系如图乙所示，忽略星球自转。求：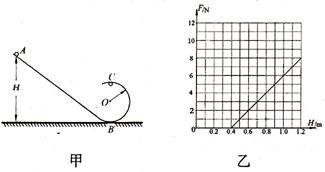

(1)圆弧轨道BC的半径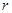；(2)该星球的第一宇宙速度。

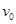如图为某游乐场内水上滑梯轨道示意图，整个轨道在同一竖直平面内，轨道表面粗糙，点A距水面的高度为H， B点距水面的高度为R，一质量为m的游客（视为质点）从A点由静止开始滑下，到B点时沿水平切线方向滑离轨道后落在水面D点， OD=2R，不计空气阻力，重力加速度为g，求：

(1) 游客滑到B点的速度v_B的大小
(2) 游客运动过程中轨道摩擦力对其所做的功W_f

如图所示，ABCD为竖立放在场强为E＝10⁴ V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的BCD部分是半径为R的半圆环，轨道的水平部分与半圆环相切，A为水平轨道上的一点，而且AB＝R＝0.2 m．把一质量m＝0.1 kg、带电量q＝10^－4 C的小球放在水平轨道的A点，由静止开始释放后，在轨道的内侧运动．(取g＝10 m/s²)求：

(1)它到达C点时的速度是多大？
(2)若让小球安全通过D点，开始释放点离B点至少多远？

光滑水平面与一半径为R＝2.5 m的竖直光滑圆轨道平滑连接，如图所示，物体可以由圆轨道底端阀门(图中未画出)进入圆轨道，水平轨道上有一轻质弹簧，其左端固定在墙壁上，右端与质量为m＝0.5 kg的小球A接触但不相连，今向左推小球A压缩弹簧至某一位置后，由静止释放小球A，测得小球A到达圆轨道最高点时对轨道的压力大小为F_N＝10 N，g＝10 m/s².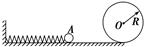

(1)求弹簧的弹性势能E_p；
(2)若弹簧的弹性势能E_p＝25 J，小球进入圆轨道后阀门关闭，通过计算说明小球会不会脱离圆轨道．若脱离，求在轨道上何处脱离(可用三角函数表示)，若不能脱离，求小球对轨道的最大与最小压力的差ΔF.

如图所示，一质量为m＝2 kg的滑块从半径为R＝0.2 m的光滑四分之一圆弧轨道的顶端A处由静止滑下，A点和圆弧对应的圆心O点等高，圆弧的底端B与水平传送带平滑相接．已知传送带匀速运行的速度为v₀＝4 m/s，B点到传送带右端C点的距离为L＝2 m．当滑块滑到传送带的右端C时，其速度恰好与传送带的速度相同．(g＝10 m/s²)，求：

(1)滑块到达底端B时对轨道的压力；
(2)滑块与传送带间的动摩擦因数μ；
(3)此过程中，由于滑块与传送带之间的摩擦而产生的热量Q.

如图所示，半径为r=0.4m的1/4圆形光滑轨道AB固定于竖直平面内，轨道与粗糙的水平地面相切于B点，CDE为固定于竖直平面内的一段内壁光滑的中空方形细管，DE段被弯成以O为圆心、半径R=0.2m的一小段圆弧，管的C端弯成与地面平滑相接，O点位于地面，OE连线竖直．可视为质点的物块b，从A点由静止开始沿轨道下滑，经地面进入细管（b横截面略小于管中空部分的横截面），b滑到E点时受到细管下壁的支持力大小等于所受重力的1/2．已知物块b的质量m = 0.4kg，g取10m/s²．

（1）求物块b滑过E点时的速度大小v_E．
（2）求物块b滑过地面BC过程中克服摩擦力做的功W_f．
（3）若将物块b静止放在B点，让另一可视为质点的物块a，从A点由静止开始沿轨道下滑，滑到B点时与b发生弹性正碰，已知a的质量M≥m，求物块b滑过E点后在地面的首次落点到O点的距离范围．

如图所示，倾角为θ=45°的粗糙平直导轨与半径为R的光滑圆环轨道相切，切点为B，整个轨道处在竖直平面内。一质量为m的小滑块从导轨上离地面高为h=3R的D处无初速下滑进入圆环轨道.接着小滑块从圆环最高点C水平飞出，恰好击中导轨上与圆心O等高的P点，不计空气阻力. 求：

（1）滑块运动到圆环最高点C时的速度的大小；
（2）滑块运动到圆环最低点时对圆环轨道压力的大小；
（3）滑块在斜面轨道BD间运动的过程中克服摩擦力做的功。

质量为m的物体由半圆形轨道顶端从静止开始释放，如图所示，A为轨道最低点，A与圆心0在同一竖直线上，已知圆弧轨道半径为R，运动到A点时，物体对轨道的压力大小为2.5mg，求此过程中物体克服摩擦力做的功。

如图所示，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细绳的下端吊一个质量为m的铁球(可视作质点)，球离地的高度h＝L．现让环与球一起以v＝的速度向右运动，在A处环被挡住而立即停止，已知A离右墙的水平距离也为L，当地的重力加速度为g，不计空气阻力．求：

(1)在环被挡住而立即停止时绳对小球的拉力大小；
(2)若在环被挡住后，细绳突然断裂，则在以后的运动过程中，球的第一次碰撞点离墙角B点的距离是多少？

“太极球”是近年来在广大市民中较流行的一种健身器材．做该项运动时，健身者半马步站立，手持太极球拍，拍上放一橡胶太极球，健身者舞动球拍时，球却不会掉落地上．现将太极球简化成如图甲所示的平板和小球，熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动，且在运动到图中的A、B、C、D位置时小球与板间无相对运动趋势．A为圆周的最高点，C为最低点，B、D与圆心O等高，圆的半径为R．已知小球的重力为1 N，不计平板的重力，且在A处板对小球的作用力为F．

(1)设小球在A处的速度大小为v，写出在A处板对小球的作用力与小球速度大小的关系式；
(2)求在C处板对小球的作用力比在A处大多少？
(3)当球运动到B、D位置时，板与水平方向需有一定的夹角θ，才能使小球在竖直面内做匀速圆周运动，请作出tan θ－F的关系图象．

如图所示，一块足够大的光滑平板放置在水平面上，能绕水平固定轴MN调节其与水平面所成的倾角。板上一根长为="0." 60m的轻细绳，它的一端系住一质量为0.2kg的小球P，另一端固定在板上的O点。先将轻绳平行于水平轴MN拉直，然后给小球一沿着平板并与轻绳垂直的初速度v₀=3.0m/s。重力加速度g=l0

(1)求当平板的倾角固定为90º，小球经过运动轨迹的最低点时轻细绳中的拉力大小；
(2)当平板的倾角固定为α时，若小球能保持在板面内作圆周运动，倾角α的值应在什么范围内？

(12分）如图所示，一半径为R的绝缘圆形轨道竖直放置，圆轨道最低点与一条水平轨道相连，轨道都是光滑的．轨道所在空间存在水平向右的匀强电场，场强为E．从水平轨道上的A点由静止释放一质量为m的带正电的小球，为使小球刚好在圆轨道内做圆周运动，求释放点A距圆轨道最低点B的距离s。已知小球受到的电场力大小等于小球重力的倍。

如图所示，竖直光滑圆轨道BCD固定在水平面AB上，轨道圆心为O，半径R=lm，轨道最低点与水平面相切于B点，C为轨道最高点，D点与圆心O等高。一质量m=1Kg的小物块，从水平面上以速度V₀竖直向上抛出，抛出的初速度v₀ =8m/s，物块从D点进入圆轨道，最终停在A点。若A、B间的距离为8m。g=l0m／s²。求：

(1)求物块运动到C点时，对轨道的压力为多大？
(2)求物块与水平面间的动摩擦因数μ。
(3)物块从B点运动到A点所用的时间。