初中数学一次函数图象与几何变换试题

一次函数 $y=\mathit{kx}+b(k\ne 0)$的图象经过点 $A(2,-6)$，且与反比例函数 $y=-\frac{12}{x}$的图象交于点 $B(a,4)$．

（1）求一次函数的解析式；

（2）将直线 $\mathit{AB}$向上平移10个单位后得到直线 $l:y_1=k_{1}x+b_1(k_1\ne 0)$， $l$与反比例函数 $y_2=\frac{6}{x}$的图象相交，求使 $y_1<y_2$成立的 $x$的取值范围．

定义：一次函数 $y=\mathit{ax}+b$ 的特征数为 $[a$ ， $b]$ ，若一次函数 $y=-2x+m$ 的图象向上平移3个单位长度后与反比例函数 $y=-\frac{3}{x}$ 的图象交于 $A$ ， $B$ 两点，且点 $A$ ， $B$ 关于原点对称，则一次函数 $y=-2x+m$ 的特征数是 $($ 　　 $)$

A．

$[2$ ， $3]$

B．

$[2$ ， $-3]$

C．

$[-2$ ， $3]$

D．

$[-2$ ， $-3]$

已知点 $P(1,2)$关于 $x$轴的对称点为 $P\text{'}$，且 $P\text{'}$在直线 $y=\mathit{kx}+3$上，把直线 $y=\mathit{kx}+3$的图象向上平移2个单位，所得的直线解析式为　　．

如图，直线 $y=-x+5$与双曲线 $y=\frac{k}{x}(x>0)$相交于 $A$， $B$两点，与 $x$轴相交于 $C$点， $\mathit{\Delta BOC}$的面积是 $\frac{5}{2}$．若将直线 $y=-x+5$向下平移1个单位，则所得直线与双曲线 $y=\frac{k}{x}(x>0)$的交点有 $($　　 $)$

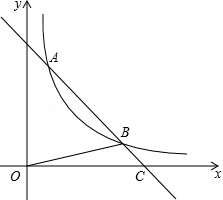
A．0个B．1个

C．2个D．0个，或1个，或2个

将直线 $y=-2x-1$向上平移两个单位，平移后的直线所对应的函数关系式为 $($　　 $)$

A． $y=-2x-5$B． $y=-2x-3$C． $y=-2x+1$D． $y=-2x+3$

一次函数 $y=\mathit{kx}+b(k\ne 0)$的图象与反比例函数 $y=\frac{m}{x}$的图象相交于 $A(2,3)$， $B(6,n)$两点．

（1）求一次函数的解析式；

（2）将直线 $\mathit{AB}$沿 $y$轴向下平移8个单位后得到直线 $l$， $l$与两坐标轴分别相交于 $M$， $N$，与反比例函数的图象相交于点 $P$， $Q$，求 $\frac{\mathit{PQ}}{\mathit{MN}}$的值．

如图，在平面直角坐标系中，一次函数 $y=2x-1$的图象分别交 $x$、 $y$轴于点 $A$、 $B$，将直线 $\mathit{AB}$绕点 $B$按顺时针方向旋转 $45°$，交 $x$轴于点 $C$，则直线 $\mathit{BC}$的函数表达式是　           　．

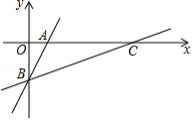
如图，在直角坐标系中，直线 $y=-\frac{1}{2}x$与反比例函数 $y=\frac{k}{x}$的图象交于关于原点对称的 $A$， $B$两点，已知 $A$点的纵坐标是3．

（1）求反比例函数的表达式；

（2）将直线 $y=-\frac{1}{2}x$向上平移后与反比例函数在第二象限内交于点 $C$，如果 $\mathit{\Delta ABC}$的面积为48，求平移后的直线的函数表达式．

在 $\mathit{\Delta ABC}$ 中， $\mathit{BC}$ 边的长为 $x$ ， $\mathit{BC}$ 边上的高为 $y$ ， $\mathit{\Delta ABC}$ 的面积为2．

（1） $y$ 关于 $x$ 的函数关系式是 　    　， $x$ 的取值范围是 　　；

（2）在平面直角坐标系中画出该函数图象；

（3）将直线 $y=-x+3$ 向上平移 $a(a>0)$ 个单位长度后与上述函数图象有且只有一个交点，请求出此时 $a$ 的值．

已知直线 $y=\mathit{kx}(k\ne 0)$经过点 $(12,-5)$，将直线向上平移 $m(m>0)$个单位，若平移后得到的直线与半径为6的 $\odot O$相交（点 $O$为坐标原点），则 $m$的取值范围为　　．

直线 $y=\mathit{kx}+b$与双曲线 $y=-\frac{6}{x}$交于 $A(-3,m)$， $B(n,-6)$两点，将直线 $y=\mathit{kx}+b$向上平移8个单位长度后，与双曲线交于 $D$， $E$两点，则 $S_{\mathit{\Delta ADE}}=$　　．

如图，在平面直角坐标系中，正比例函数 $y=\mathit{kx}$的图象与反比例函数 $y=\frac{m}{x}$的图象都过点 $A(2,2)$，将直线 $\mathit{OA}$向上平移4个单位长度后，与反比例函数图象交于点 $C$，与 $x$轴交于点 $B$，连接 $\mathit{AB}$， $\mathit{AC}$，则 $\mathit{\Delta ABC}$的面积为　　．

将函数 $y=-2x$的图象向下平移3个单位，所得图象对应的函数关系式为 $($　　 $)$

A． $y=-2(x+3)$B． $y=-2(x-3)$C． $y=-2x+3$D． $y=-2x-3$

将函数 $y=-2x$的图象向下平移3个单位，所得图象对应的函数关系式为 $($　　 $)$

A． $y=-2(x+3)$B． $y=-2(x-3)$C． $y=-2x+3$D． $y=-2x-3$

将直线 $y=-2x$向上平移1个单位长度，平移后直线的解析式为　　．