初中数学一次函数图象与几何变换试题

如图，在平面直角坐标系中，直线 $y=x$与反比例函数 $y=\frac{4}{x}(x>0)$的图象交于点 $A$，将直线 $y=x$沿 $y$轴向上平移 $b$个单位长度，交 $y$轴于点 $B$，交反比例函数图象于点 $C$．若 $\mathit{OA}=2\mathit{BC}$，则 $b$的值为 $($　　 $)$

A．1B．2C．3D．4

将直线 $y=\frac{3}{2}x-1$ 沿 $x$ 轴向左平移4个单位，则平移后的直线与 $y$ 轴交点的坐标是 $($ 　　 $)$

A．

$(0,5)$

B．

$(0,3)$

C．

$(0,-5)$

D．

$(0,-7)$

将函数 $y=-2x$的图象向下平移3个单位，所得图象对应的函数关系式为 $($　　 $)$

A． $y=-2(x+3)$B． $y=-2(x-3)$C． $y=-2x+3$D． $y=-2x-3$

在平面直角坐标系中，垂直于轴的直线分别与函数和的图象相交于，两点．若平移直线，可以使，都在轴的下方，则实数的取值范围是　     　．

在平面直角坐标系中，一次函数的图象由函数的图象平移得到，且经过点．

（1）求这个一次函数的解析式；

（2）当时，对于的每一个值，函数的值大于一次函数的值，直接写出的取值范围．

如图，一次函数 $y=x+\sqrt{2}$ 的图象与 $x$ 轴、 $y$ 轴分别交于点 $A$ ， $B$ ，把直线 $\mathit{AB}$ 绕点 $B$ 顺时针旋转 $30°$ 交 $x$ 轴于点 $C$ ，则线段 $\mathit{AC}$ 长为 $($ 　　 $)$

A．

$\sqrt{6}+\sqrt{2}$

B．

$3\sqrt{2}$

C．

$2+\sqrt{3}$

D．

$\sqrt{3}+\sqrt{2}$

将直线 $y=-2x$向上平移1个单位长度，平移后直线的解析式为　　．

如图，直线 $y=-x+5$与双曲线 $y=\frac{k}{x}(x>0)$相交于 $A$， $B$两点，与 $x$轴相交于 $C$点， $\mathit{\Delta BOC}$的面积是 $\frac{5}{2}$．若将直线 $y=-x+5$向下平移1个单位，则所得直线与双曲线 $y=\frac{k}{x}(x>0)$的交点有 $($　　 $)$

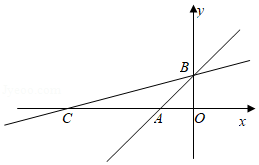
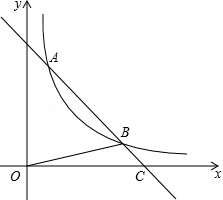
A．0个B．1个

C．2个D．0个，或1个，或2个

函数图象在探索函数的性质中有非常重要的作用，下面我们就一类特殊的函数展开探索．画函数的图象，经历分析解析式、列表、描点、连线过程得到函数图象如图所示；经历同样的过程画函数和的图象如图所示．

					0	1	2	3
					0

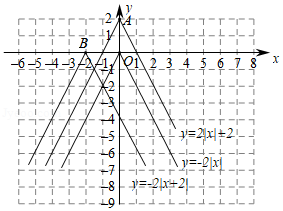
（1）观察发现：三个函数的图象都是由两条射线组成的轴对称图形；三个函数解析式中绝对值前面的系数相同，则图象的开口方向和形状完全相同，只有最高点和对称轴发生了变化．写出点，的坐标和函数的对称轴．

（2）探索思考：平移函数的图象可以得到函数和的图象，分别写出平移的方向和距离．

（3）拓展应用：在所给的平面直角坐标系内画出函数的图象．若点，和，在该函数图象上，且，比较，的大小．

直线y=2x经过平移可以得到直线y=2x-2的是（  ）

A．向左平移1个单位	B．向左平移2个单位
C．向右平移1个单位	D．向上平移 2个单位

将直线 $y=-6x$向下平移2个单位长度，平移后直线的解析式为 　　．

将直线 $y=5x$ 向下平移2个单位长度，所得直线的表达式为 $($ 　　 $)$

A．

$y=5x-2$

B．

$y=5x+2$

C．

$y=5(x+2)$

D．

$y=5(x-2)$

将直线 $y=-x+1$向左平移 $m(m>0)$个单位后，经过点 $(1,-3)$，则 $m$的值为 　　．

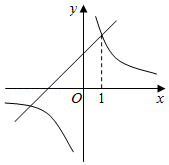
如图，一次函数 $y=x+2$的图象与反比例函数 $y=\frac{k}{x}$的图象相交，其中一个交点的横坐标是1．

（1）求 $k$的值；

（2）若将一次函数 $y=x+2$的图象向下平移4个单位长度，平移后所得到的图象与反比例函数 $y=\frac{k}{x}$的图象相交于 $A$， $B$两点，求此时线段 $\mathit{AB}$的长．

在平面直角坐标系 $\mathit{xOy}$中，一次函数 $y=\mathit{kx}+b(k\ne 0)$的图象由函数 $y=\frac{1}{2}x$的图象向下平移1个单位长度得到．

（1）求这个一次函数的解析式；

（2）当 $x>-2$时，对于 $x$的每一个值，函数 $y=\mathit{mx}(m\ne 0)$的值大于一次函数 $y=\mathit{kx}+b$的值，直接写出 $m$的取值范围．