初中数学二次函数的应用解答题

某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．

（1）求y与x之间的函数关系式；

（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？

（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？

夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务．为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．

（1）设第 $x$天生产空调 $y$台，直接写出 $y$与 $x$之间的函数解析式，并写出自变量 $x$的取值范围．

（2）若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第 $x$天的利润为 $W$元，试求 $W$与 $x$之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．

科技馆是少年儿童节假日游玩的乐园．

如图所示，图中点的横坐标x表示科技馆从8：30开门后经过的时间（分钟），纵坐标y表示到达科技馆的总人数．图中曲线对应的函数解析式为 $y=\left\{\begin{array}{c}a{x}^2,0\le x\le 30\\ b{(}^x+n,30\le x\le 90\end{array}\right.$，10：00之后来的游客较少可忽略不计．

（1）请写出图中曲线对应的函数解析式；

（2）为保证科技馆内游客的游玩质量，馆内人数不超过684人，后来的人在馆外休息区等待．从10：30开始到12：00馆内陆续有人离馆，平均每分钟离馆4人，直到馆内人数减少到624人时，馆外等待的游客可全部进入．请问馆外游客最多等待多少分钟？

“绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行．某自行车店在销售某型号自行车时，以高出进价的 $50\%$标价．已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同．

（1）求该型号自行车的进价和标价分别是多少元？

（2）若该型号自行车的进价不变，按（1）中的标价出售，该店平均每月可售出51辆；若每辆自行车每降价20元，每月可多售出3辆，求该型号自行车降价多少元时，每月获利最大？最大利润是多少？

某宾馆有50个房间供游客居住，当每个房间定价120元时，房间会全部住满，当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间定价增加10x元（x为整数）．

（1）直接写出每天游客居住的房间数量y与x的函数关系式．

（2）设宾馆每天的利润为W元，当每间房价定价为多少元时，宾馆每天所获利润最大，最大利润是多少？

（3）某日，宾馆了解当天的住宿的情况，得到以下信息：①当日所获利润不低于5000元，②宾馆为游客居住的房间共支出费用没有超过600元，③每个房间刚好住满2人．问：这天宾馆入住的游客人数最少有多少人？

端午节前夕，三位同学到某超市调研一种进价为80元的粽子礼盒的销售情况，请根据小梅提供的信息，解答小慧和小杰提出的问题．（价格取正整数）

某商场试销 A、 B两种型号的台灯，下表是两次进货情况统计：

进货情况 进货次数	进货数量（台）		进货资金（元）
	A	B
第一次	5	3	230
第二次	10	4	440

（1）求 A、 B两种型号台灯的进价各为多少元？

（2）经试销发现， A型号台灯售价 x（元）与销售数量 y（台）满足关系式2 x+ y＝140，此商场决定两种型号台灯共进货100台，并一周内全部售出，若 B型号台灯售价定为20元，求 A型号台灯售价定为多少时，商场可获得最大利润？并通过计算说明商场获得最大利润时的进货方案．

温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件利润减少2元．设每天安排 $x$人生产乙产品．

（1）根据信息填表：

产品种类	每天工人数（人 $)$	每天产量（件 $)$	每件产品可获利润（元 $)$
甲			15
乙	$x$	$x$

（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．

（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润 $W$（元 $)$的最大值及相应的 $x$值．

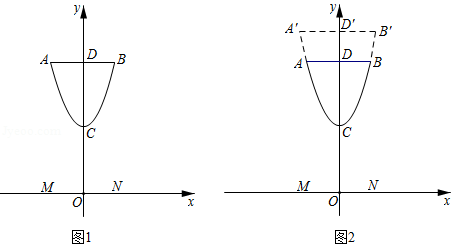
小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体 $\mathit{ACB}$ 是抛物线的一部分，抛物线的顶点 $C$ 在 $y$ 轴上，杯口直径 $\mathit{AB}=4$ ，且点 $A$ ， $B$ 关于 $y$ 轴对称，杯脚高 $\mathit{CO}=4$ ，杯高 $\mathit{DO}=8$ ，杯底 $\mathit{MN}$ 在 $x$ 轴上．

（1）求杯体 $\mathit{ACB}$ 所在抛物线的函数表达式（不必写出 $x$ 的取值范围）；

（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯体 $A\text{'}\mathit{CB}\text{'}$ 所在抛物线形状不变，杯口直径 $A\text{'}B\text{'}//\mathit{AB}$ ，杯脚高 $\mathit{CO}$ 不变，杯深 $\mathit{CD}\text{'}$ 与杯高 $\mathit{OD}\text{'}$ 之比为0.6，求 $A\text{'}B\text{'}$ 的长．

今年以来，我市接待的游客人数逐月增加，据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人．

（1）求四月和五月这两个月中该景区游客人数平均每月增长百分之几；

（2）若该景区仅有 $A$ ， $B$ 两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	$A$	$B$	$A$ 和     $B$
门票价格	100元     $/$ 人	80元     $/$ 人	160元     $/$ 人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票．

①若丙种门票价格下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

某商场购进甲、乙两种商品共100箱，全部售完后，甲商品共盈利900元，乙商品共盈利400元，甲商品比乙商品每箱多盈利5元．

（1）求甲、乙两种商品每箱各盈利多少元？

（2）甲、乙两种商品全部售完后，该商场又购进一批甲商品，在原每箱盈利不变的前提下，平均每天可卖出100箱．如调整价格，每降价1元，平均每天可多卖出20箱，那么当降价多少元时，该商场利润最大？最大利润是多少？

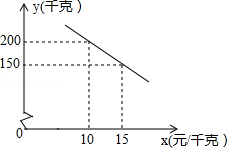
某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚，到了收获季节，已知该蜜柚的成本价为8元 $/$千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量 $y$（千克）与销售单价 $x$（元 $/$千克）之间的函数关系如图所示．

（1）求 $y$与 $x$的函数关系式，并写出 $x$的取值范围；

（2）当该品种的蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

（3）某农户今年共采摘蜜柚4800千克，该品种蜜柚的保质期为40天，根据（2）中获得最大利润的方式进行销售，能否销售完这批蜜柚？请说明理由．

结合西昌市创建文明城市要求，某小区业主委员会决定把一块长 $80m$，宽 $60m$的矩形空地建成花园小广场，设计方案如图所示，阴影区域为绿化区（四块绿化区为全等的直角三角形），空白区域为活动区，且四周出口宽度一样，其宽度不小于 $36m$，不大于 $44m$，预计活动区造价60元 $/m^2$，绿化区造价50元 $/m^2$，设绿化区域较长直角边为 $\mathit{xm}$．

（1）用含 $x$的代数式表示出口的宽度；

（2）求工程总造价 $y$与 $x$的函数关系式，并直接写出 $x$的取值范围；

（3）如果业主委员会投资28.4万元，能否完成全部工程？若能，请写出 $x$为整数的所有工程方案；若不能，请说明理由．

（4）业主委员会决定在（3）设计的方案中，按最省钱的一种方案，先对四个绿化区域进行绿化，在实际施工中，每天比原计划多绿化 $11m^2$，结果提前4天完成四个区域的绿化任务，问原计划每天绿化多少 $m^2$．

某公司研发了一款成本为60元的保温饭盒，投放市场进行试销售，按物价部门规定，其销售单价不低于成本，但销售利润不高于 $65\%$，市场调研发现，保温饭盒每天的销售数量 $y$（个 $)$与销售单价 $x$（元 $)$满足一次函数关系；当销售单价为70元时，销售数量为160个；当销售单价为80元时，销售数量为140个（利润率 $=\frac{\mathit{利润}}{\mathit{成本}}\times 100\backslash \%)$

（1）求 $y$与 $x$之间的函数关系式；

（2）当销售单价定为多少元时，公司每天获得利润最大，最大利润为多少元？

某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销x件．已知产销两种产品的有关信息如表：

产品	每件售价（万元）	每件成本（万元）	每年其他费用（万元）	每年最大产销量（件）
甲	6	a	20	200
乙	20	10	40+0.05x^2	80

其中a为常数，且 $3\le a\le 5$。

（1）若产销甲、乙两种产品的年利润分别为y₁万元、y₂万元，直接写出y₁、y₂与x的函数关系式；

（2）分别求出产销两种产品的最大年利润；

（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．