如图, 的顶点坐标分别为 , , ,动点 、 同时从点 出发,分别沿 轴正方向和 轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点 到达点 时点 、 同时停止运动.过点 作 分别交 、 于点 、 ,连接 、 .设运动时间为 (秒 .
(1)求点 的坐标(用含 的式子表示);
(2)求四边形 面积的最大值或最小值;
(3)是否存在这样的直线 ,总能平分四边形 的面积?如果存在,请求出直线 的解析式;如果不存在,请说明理由;
(4)连接 ,当 时,求点 到 的距离.

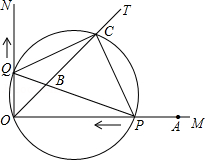
如图,已知 , 是 的平分线, 是射线 上一点, .动点 从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点 从点 出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点 .经过 、 、 三点作圆,交 于点 ,连接 、 .设运动时间为 ,其中 .
(1)求 的值;
(2)是否存在实数 ,使得线段 的长度最大?若存在,求出 的值;若不存在,说明理由.
(3)求四边形 的面积.
某厂按用户的月需求量(件
完成一种产品的生产,其中
,每件的售价为18万元,每件的成本
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(件
成反比,经市场调研发现,月需求量
与月份
为整数,
,符合关系式
为常数),且得到了表中的数据.
月份 |
1 |
2 |
成本 |
11 |
12 |
需求量 |
120 |
100 |
(1)求与
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第个月和第
个月的利润相差最大,求
.
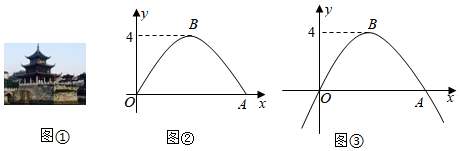
甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
(1)按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;
(2)一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处,有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平).
(3)如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.
如图,在平面直角坐标系中,一次函数 的图象与 轴和 轴分别相交于 、 两点.动点 从点 出发,在线段 上以每秒3个单位长度的速度向点 作匀速运动,到达点 停止运动,点 关于点 的对称点为点 ,以线段 为边向上作正方形 .设运动时间为 秒.
(1)当 秒时,点 的坐标是 ;
(2)在运动过程中,设正方形 与 重叠部分的面积为 ,求 与 的函数表达式;
(3)若正方形 对角线的交点为 ,请直接写出在运动过程中 的最小值.

某市计划在十二年内通过公租房建设,解决低收入人群的住房问题.已知前7年,每年竣工投入使用的公租房面积 y(单位:百万平方米),与时间 x(第 x年)的关系构成一次函数,(1≤ x≤7且 x为整数),且第一和第三年竣工投入使的公租房面积分别为 和 百万平方米;后5年每年竣工投入使用的公租房面积 y(单位:百万平方米),与时间 x(第 x年)的关系是 y=﹣ x+ (7< x≤12且 x为整数).
(1)已知第6年竣工投入使用的公租房面积可解决20万人的住房问题,如果人均住房面积,最后一年要比第6年提高20%,那么最后一年竣工投入使用的公租房面积可解决多少万人的住房问题?
(2)受物价上涨等因素的影响,已知这12年中,每年竣工投入使用的公租房的租金各不相同,且第一年,一年38元/ m 2,第二年,一年40元/ m 2,第三年,一年42元/ m 2,第四年,一年44元/ m 2……以此类推,分析说明每平方米的年租金和时间能否构成函数,如果能,直接写出函数解析式;
(3)在(2)的条件下,假设每年的公租房当年全部出租完,写出这12年中每年竣工投入使用的公租房的年租金 W关于时间 x的函数解析式,并求出 W的最大值(单位:亿元).如果在 W取得最大值的这一年,老张租用了58 m 2的房子,计算老张这一年应交付的租金.
如图,在 中, , , ,点 , 分别是边 , 上的动点(点 不与 , 重合),且 ,过点 作 的平行线 ,交 于点 ,连接 ,设 为 .
(1)试说明不论 为何值时,总有 ;
(2)是否存在一点 ,使得四边形 为平行四边形,试说明理由;
(3)当 为何值时,四边形 的面积最大,并求出最大值.

已知某厂以 小时 千克的速度匀速生产某种产品(生产条件要求 ,且每小时可获得利润 元.
(1)某人将每小时获得的利润设为 元,发现 时, ,所以得出结论:每小时获得的利润,最少是180元,他是依据什么得出该结论的,用你所学数学知识帮他进行解析说明;
(2)若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;
(3)要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
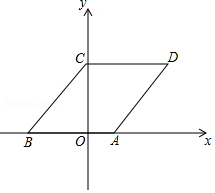
如图,在平面直角坐标系中,菱形 的边 在 轴上,点 坐标 ,点 在 轴正半轴上,且 ,点 从原点 出发,以每秒一个单位长度的速度沿 轴正方向移动,移动时间为 秒,过点 作平行于 轴的直线 ,直线 扫过四边形 的面积为 .
(1)求点 坐标.
(2)求 关于 的函数关系式.
(3)在直线 移动过程中, 上是否存在一点 ,使以 、 、 为顶点的三角形是等腰直角三角形?若存在,直接写出 点的坐标;若不存在,请说明理由.
如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 (千米)与时间 (分钟)的函数关系用图3表示,其中:“ 时甲地‘交叉潮’的潮头离乙地12千米”记为点 ,点 坐标为 ,曲线 可用二次函数 , 是常数)刻画.
(1)求 的值,并求出潮头从甲地到乙地的速度;
(2) 时,小红骑单车从乙地出发,沿江边公路以0.48千米 分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米 分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 , 是加速前的速度).
如图1,直线 与 轴交于点 ,与 轴交于点 ,点 是线段 上一动点 .以点 为圆心, 长为半径作 交 轴于另一点 ,交线段 于点 ,连接 并延长交 于点 .

(1)求直线 的函数表达式和 的值;
(2)如图2,连接 ,当 时,
①求证: ;
②求点 的坐标;
(3)当点 在线段 上运动时,求 的最大值.
如图,在矩形 中, , .动点 从点 出发沿折线 向终点 运动,在边 上以 的速度运动;在边 上以 的速度运动,过点 作线段 与射线 相交于点 ,且 ,连接 , .设点 的运动时间为 , 与 重合部分图形的面积为 .
(1)当点 与点 重合时,直接写出 的长;
(2)当点 在边 上运动时,直接写出 的长(用含 的代数式表示);
(3)求
关于
的函数解析式,并写出自变量
的取值范围.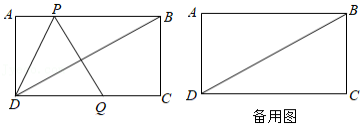
因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天销售量 (桶 与销售单价 (元 之间满足一次函数关系,其图象如图所示.
(1)求 与 之间的函数表达式;
(2)每桶消毒液的销售价定为多少元时,药店每天获得的利润最大,最大利润是多少元?(利润 销售价 进价)

某水果商店销售一种进价为40元 千克的优质水果,若售价为50元 千克,则一个月可售出500千克;若售价在50元 千克的基础上每涨价1元,则月销售量就减少10千克.
(1)当售价为55元 千克时,每月销售水果多少千克?
(2)当月利润为8750元时,每千克水果售价为多少元?
(3)当每千克水果售价为多少元时,获得的月利润最大?
试题篮
()