【观察】 , , , , , , , , , , , , .
【发现】根据你的阅读回答问题:
(1)上述内容中,两数相乘,积的最大值为 ;
(2)设参与上述运算的第一个因数为 ,第二个因数为 ,用等式表示 与 的数量关系是 .
【类比】观察下列两数的积: , , , , , , , , , , .
猜想 的最大值为 ,并用你学过的知识加以证明.
小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为 (元 ,日销量为 (件 ,日销售利润为 (元 .
(1)求 与 的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润 (元 与销售单价 (元 的函数关系式,当 为何值时,日销售利润最大,并求出最大利润.
某服装店以每件30元的价格购进一批 恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设 恤的销售单价提高 元.
(1)服装店希望一个月内销售该种 恤能获得利润3360元,并且尽可能减少库存,问 恤的销售单价应提高多少元?
(2)当销售单价定为多少元时,该服装店一个月内销售这种 恤获得的利润最大?最大利润是多少元?
2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价 (元 与月份 ,且 为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本 (元 与月份 ,且 为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份 |
|
3 |
4 |
5 |
6 |
|
售价 元 |
|
12 |
14 |
16 |
18 |
|
(1)求 与 之间的函数关系式.
(2)求 与 之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为 (元 ,求 与 之间的函数关系式,哪个月份销售每千克猪肉所获得的利润最大?最大利润是多少元?

铁岭市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量 (千克)与每千克降价 (元 之间满足一次函数关系,其图象如图所示:
(1)求 与 之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
(3)该干果每千克降价多少元时,商贸公司获利最大?最大利润是多少元?

某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于 ,市场调研发现,在一段时间内,每天销售数量 (个 与销售单价 (元 符合一次函数关系,如图所示:
(1)根据图象,直接写出 与 的函数关系式.
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?

课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为 ,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为 时,透光面积最大值约为 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为 ,利用图3,解答下列问题:
(1)若 为 ,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.

鹏鹏童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价1元,每星期可多卖10件.已知该款童装每件成本30元.设该款童装每件售价 元,每星期的销售量为 件.
(1)求 与 之间的函数关系式(不求自变量的取值范围);
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)①当每件童装售价定为多少元时,该店一星期可获得3910元的利润?
②若该店每星期想要获得不低于3910元的利润,则每星期至少要销售该款童装多少件?
麦积山石窟是世界文化遗产,国家 级旅游景区,中国四大石窟之一.在2018年中国西北旅游营销大会暨旅游装备展上,商家按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按此进价进货、标价销售,商家每天可售出该工艺品100件;若每件工艺品降价1元,则每天可多售出该工艺品4件.问:每件工艺品降价多少元销售,每天获得的利润最大?获得的最大利润是多少元?
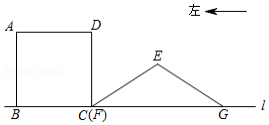
如图所示,在正方形 和 中, , ,点 、 、 、 在同一直线 上.当点 、 重合时, 以 的速度沿直线 向左开始运动, 秒后正方形 与 重合部分的面积为 .请解答下列问题:
(1)当 秒时,求 的值;
(2)当 秒时,求 的值;
(3)当5秒 秒时,求 与 的函数关系式,并求出 的最大值.
某公司设计了一款产品,每件成本是50元,在试销期间,据市场调查,销售单价是60元时,每天的销量是250件,而销售单价每增加1元,每天会少售出5件,公司决定销售单价 (元 不低于60元,而市场要求 不得超过100元.
(1)求出每天的销售量 (件 与销售单价 (元 之间的函数关系式,并写出 的取值范围;
(2)求出每天的销售利润 (元 与销售单价 (元 之间的函数关系式,并求出当 为多少时,每天的销售利润最大,并求出最大值;
(3)若该公司要求每天的销售利润不低于4000元,但每天的总成本不超过6250元,则销售单价 最低可定为多少元?
随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳 葫芦岛海滨观光一日游”项目,团队人均报名费用 (元 与团队报名人数 (人 之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为 (元 .
(1)直接写出当 时, 与 之间的函数关系式及自变量 的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?

某商场销售一种商品的进价为每件30元,销售过程中发现月销售量 (件 与销售单价 (元 之间的关系如图所示.
(1)根据图象直接写出 与 之间的函数关系式.
(2)设这种商品月利润为 (元 ,求 与 之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
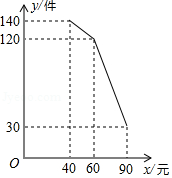
传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第 天生产的粽子数量为 只, 与 满足如下关系:
(1)李明第几天生产的粽子数量为280只?
(2)如图,设第 天生产的每只粽子的成本是 元, 与 之间的关系可用图中的函数图象来刻画.若李明第 天创造的利润为 元,求 与 之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润 出厂价 成本)

结合西昌市创建文明城市要求,某小区业主委员会决定把一块长 ,宽 的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于 ,不大于 ,预计活动区造价60元 ,绿化区造价50元 ,设绿化区域较长直角边为 .
(1)用含 的代数式表示出口的宽度;
(2)求工程总造价 与 的函数关系式,并直接写出 的取值范围;
(3)如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出 为整数的所有工程方案;若不能,请说明理由.
(4)业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化 ,结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少 .

试题篮
()