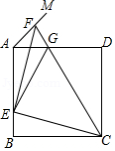
如图,正方形 的边长为 ,点 在边 上运动(不与点 , 重合), ,点 在射线 上,且 , 与 相交于点 ,连接 、 、 .则下列结论:
① ;
② 的周长为 ;
③ ;
④ 的面积的最大值是 ;
⑤当 时, 是线段 的中点.
其中正确的结论是
| A. |
①②③ |
B. |
②④⑤ |
C. |
①③④ |
D. |
①④⑤ |
某商店以每件50元的价格购进一批新型产品,如果按每件60元出售,那么每周可销售500件.根据市场规律,这种产品的销售单价每提高1元,其销售量每周相应减少10件,但每件产品的销售单价不低于60元,且不能高于85元,设每周的销售量为 (件 ,这种产品的销售单价为 (元 ,解答下列问题:
(1)请直接写出 与 之间的函数关系式;
(2)商家要想每周获得8000元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每周获得的销售利润最大?最大利润是多少元?
某服装店以每件30元的价格购进一批 恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设 恤的销售单价提高 元.
(1)服装店希望一个月内销售该种 恤能获得利润3360元,并且尽可能减少库存,问 恤的销售单价应提高多少元?
(2)当销售单价定为多少元时,该服装店一个月内销售这种 恤获得的利润最大?最大利润是多少元?
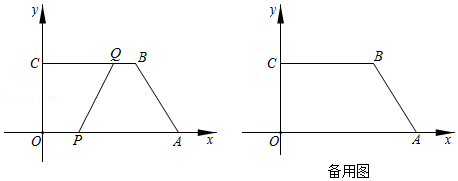
如图,在平面直角坐标系中,四边形的顶点坐标分别为
,
,
,
.动点
从点
出发,以每秒3个单位长度的速度沿边
向终点
运动;动点
从点
同时出发,以每秒2个单位长度的速度沿边
向终点
运动.设运动的时间为
秒,
.
(1)直接写出关于
的函数解析式及
的取值范围: ;
(2)当时,求
的值;
(3)连接交
于点
,若双曲线
经过点
,问
的值是否变化?若不变化,请求出
的值;若变化,请说明理由.
某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量 (本 与每本纪念册的售价 (元 之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出 与 的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为 元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
有一块形状如图的五边形余料,
,
,
,
,
,要在这块余料中截取一块矩形材料,其中一条边在
上,并使所截矩形材料的面积尽可能大.
(1)若所截矩形材料的一条边是或
,求矩形材料的面积.
(2)能否截出比(1)中更大面积的矩形材料?如果能,求出这些矩形材料面积的最大值;如果不能,说明理由.

辰星旅游度假村有甲种风格客房15间,乙种风格客房20间.按现有定价:若全部入住,一天营业额为8500元;若甲、乙两种风格客房均有10间入住,一天营业额为5000元.
(1)求甲、乙两种客房每间现有定价分别是多少元?
(2)度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会有两个房间空闲.如果游客居住房间,度假村需对每个房间每天支出80元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润最大,最大利润是多少元?
如图,在正方形中,
,
为对角线
上一动点,连接
,
,过
点作
,交直线
于点
.
点从
点出发,沿着
方向以每秒
的速度运动,当点
与点
重合时,运动停止.设
的面积为
,
点的运动时间为
秒.

(1)求证:;
(2)求与
之间关系的函数表达式,并写出自变量
的取值范围;
(3)求面积的最大值.
如图,在平面直角坐标系中,已知 A(﹣3,﹣2), B(0,﹣2), C(﹣3,0), M是线段 AB上的一个动点,连接 CM,过点 M作 MN⊥ MC交 y轴于点 N,若点 M、 N在直线 y= kx+ b上,则 b的最大值是( )

| A. |
﹣ |
B. |
﹣ |
C. |
﹣1 |
D. |
0 |
交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征.其中流量 (辆 小时)指单位时间内通过道路指定断面的车辆数;速度 (千米 小时)指通过道路指定断面的车辆速度;密度 (辆 千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量 与速度 之间关系的部分数据如下表:
速度 (千米 小时) |
|
5 |
10 |
20 |
32 |
40 |
48 |
|
流量 (辆 小时) |
|
550 |
1000 |
1600 |
1792 |
1600 |
1152 |
|
(1)根据上表信息,下列三个函数关系式中,刻画 , 关系最准确的是 (只填上正确答案的序号)
① ;② ;③ .
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知 , , 满足 ,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当 时道路出现轻度拥堵.试分析当车流密度 在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离 (米 均相等,求流量 最大时 的值.
如图,在边长为 的正方形 中,点 、 、 、 分别从点 、 、 、 同时出发,均以 的速度向点 、 、 、 匀速运动,当点 到达点 时,四个点同时停止运动,在运动过程中,当运动时间为 时,四边形 的面积最小,其最小值是 .

某厂商投产一种新型科技产品,每件制造成本为18元,试销过程中发现,每月销售量 y(万件)与销售单价 x(元)之间的关系可以近似地看作一次函数 y=﹣2 x+100
(1)写出每月的利润 L(万元)与销售单价 x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得312万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种科技产品的销售单价不能高于32元,如果厂商要获得每月不低于312万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
某市计划在十二年内通过公租房建设,解决低收入人群的住房问题.已知前7年,每年竣工投入使用的公租房面积 y(单位:百万平方米),与时间 x(第 x年)的关系构成一次函数,(1≤ x≤7且 x为整数),且第一和第三年竣工投入使的公租房面积分别为 和 百万平方米;后5年每年竣工投入使用的公租房面积 y(单位:百万平方米),与时间 x(第 x年)的关系是 y=﹣ x+ (7< x≤12且 x为整数).
(1)已知第6年竣工投入使用的公租房面积可解决20万人的住房问题,如果人均住房面积,最后一年要比第6年提高20%,那么最后一年竣工投入使用的公租房面积可解决多少万人的住房问题?
(2)受物价上涨等因素的影响,已知这12年中,每年竣工投入使用的公租房的租金各不相同,且第一年,一年38元/ m 2,第二年,一年40元/ m 2,第三年,一年42元/ m 2,第四年,一年44元/ m 2……以此类推,分析说明每平方米的年租金和时间能否构成函数,如果能,直接写出函数解析式;
(3)在(2)的条件下,假设每年的公租房当年全部出租完,写出这12年中每年竣工投入使用的公租房的年租金 W关于时间 x的函数解析式,并求出 W的最大值(单位:亿元).如果在 W取得最大值的这一年,老张租用了58 m 2的房子,计算老张这一年应交付的租金.
如图1,在平面直角坐标系中,四边形 各顶点的坐标分别为 , , 、 , , ,动点 与 同时从 点出发,运动时间为 秒,点 沿 方向以1单位长度 秒的速度向点 运动,点 沿折线 运动,在 、 、 上运动的速度分别为3, , (单位长度 秒),当 、 中的一点到达 点时,两点同时停止运动.
(1)求 所在直线的函数表达式;
(2)如图2,当点 在 上运动时,求 的面积 关于 的函数表达式及 的最大值;
(3)在 、 的运动过程中,若线段 的垂直平分线经过四边形 的顶点,求相应的 值.

试题篮
()