如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
如图,在 中, ,点 是斜边 上一点,且 .
(1)作 的平分线,交 于点 ;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接 ,求证: .

如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,
(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
如图,O为直线AB上一点,将直角三角板OCD的直角顶点放在点O处.已知∠AOC的度数比∠BOD的度数的3倍多10°.

(1)求∠BOD的度数.
(2)若OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.
如图,已知
与
互为余角,且
,
平分
,
平分
.

(1)求
的度数;
(2)如果已知中
,其他条件不变,求
的度数;
(3)如果已知中
,其他条件不变,求
的度数;
(4)从(1)、(2)、(3)中你能看出有什么规律.
已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠COE=40°时,求∠AOB的度数.
解:∵OE是∠COB的平分线,
∴∠COB=(理由:).
∵∠COE=40°,
∴.
∵∠AOC=,
∴∠AOB=∠AOC+=110°.
如图,已知A、O、B三点在同一条直线上,
平分
,
平分
.

(1)若
,求
的度数;
(2)若
,求
的度数;
(3)图中是否有互余的角?若有请写出所有互余的角.
(1)如图①,∠AOB=60°,OD平分∠BOC,OE平分∠AOC,则∠EOD=_________度;
(2)若∠AOB=90°,其它条件不变,则∠EOD=__________;
(3)若∠AOB=α,其它条件不变,则∠EOD=_________________.
类比应用:
(4)如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为_____________,并写出求解过程.
如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.
(1)求∠AOG的度数;
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?请说明理由.
如图,已知四边形ABCD中,∠C=∠D=90°,AE平分∠DAB,BE平分∠ABC,且E在D上.
(1)求∠AEB;
(2)求证:DE=CE.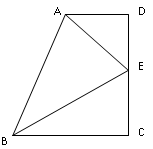
试题篮
()