如图,将矩形ABCD沿AF折叠,使点D落在BC边上的点E处,过点E作 交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若 , ,求BE的长.

如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
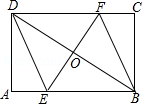
如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.

如图,矩形 ABCD中, AB> AD,把矩形沿对角线 AC所在直线折叠,使点 B落在点 E处, AE交 CD于点 F,连接 DE.
(1)求证:△ ADE≌△ CED;
(2)求证:△ DEF是等腰三角形.
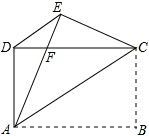
如图,矩形 ABCD中,过对角线 BD中点 O的直线分别交 AB, CD边于点 E、 F.
(1)求证:四边形 BEDF是平行四边形;
(2)只需添加一个条件,即 ,可使四边形 BEDF为菱形.

如图,在矩形 ABCD中, AB=3, BC=5, E是 AD上的一个动点. 
(1)如图1,连接 BD, O是对角线 BD的中点,连接 OE.当 OE= DE时,求 AE的长;
(2)如图2,连接 BE, EC,过点 E作 EF⊥ EC交 AB于点 F,连接 CF,与 BE交于点 G.当 BE平分∠ ABC时,求 BG的长;
(3)如图3,连接 EC,点 H在 CD上,将矩形 ABCD沿直线 EH折叠,折叠后点 D落在 EC上的点 D'处,过点 D′作 D′ N⊥ AD于点 N,与 EH交于点 M,且 AE=1.
①求 的值;
②连接 BE,△ D' MH与△ CBE是否相似?请说明理由.
如图,在四边形 ABCD中, AD∥ BC,∠ ABC=90°, AB= AD,连接 BD,点 E在 AB上,且∠ BDE=15°, DE=4 , DC=2 .
(1)求 BE的长;
(2)求四边形 DEBC的面积.
(注意:本题中的计算过程和结果均保留根号)

阅读理解:
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把 的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形度是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, 之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且 ,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为 ,平行四边形A1B1C1D1的面积为 ,试求∠A1E1B1+∠A1D1B1的度数.

如图,在矩形 ABCD中, AB=3, BC=4,将矩形 ABCD绕点 C按顺时针方向旋转α角,得到矩形 A' B' C' D', B' C与 AD交于点 E, AD的延长线与 A' D'交于点 F.

(1)如图①,当α=60°时,连接 DD',求 DD'和 A' F的长;
(2)如图②,当矩形 A' B' CD'的顶点 A'落在 CD的延长线上时,求 EF的长;
(3)如图③,当 AE= EF时,连接 AC, CF,求 AC• CF的值.
如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.
(Ⅰ)若△PCD是等腰三角形时,求AP的长;
(Ⅱ)若 ,求CF的长.
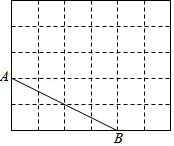
如图,在边长为1的正方形组成的 方格中,点
方格中,点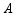 ,
,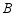 都在格点上.
都在格点上.
(1)在给定的方格中将线段 平移到
平移到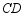 ,使得四边形
,使得四边形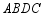 是矩形,且点
是矩形,且点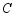 ,
,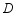 都落在格点上.画出四边形
都落在格点上.画出四边形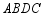 ,并叙述线段
,并叙述线段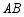 的平移过程;
的平移过程;
(2)在方格中画出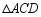 关于直线
关于直线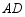 对称的
对称的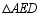 ;
;
(3)直接写出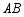 与
与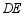 的交点
的交点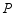 到线段
到线段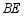 的距离.
的距离.
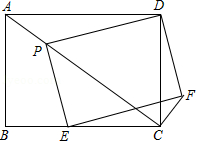
在矩形ABCD中,E为CD的中点,H为BE上的一点, ,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: ;
(2)若∠CGF=90°,求 的值.

如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=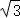 ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)

如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知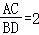 ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.

试题篮
()