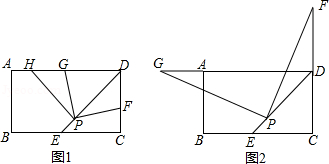
如图1,在矩形中,
,
,
是
边上一点,连接
,将矩形
沿
折叠,顶点
恰好落在
边上点
处,延长
交
的延长线于点
.
(1)求线段的长;
(2)如图2,,
分别是线段
,
上的动点(与端点不重合),且
,设
,
.
①写出关于
的函数解析式,并求出
的最小值;
②是否存在这样的点,使
是等腰三角形?若存在,请求出
的值;若不存在,请说明理由.

在直角坐标系中,过原点 及点 , 作矩形 、连接 ,点 为 的中点,点 是线段 上的动点,连接 ,作 ,交 于点 ,连接 .已知点 从 点出发,以每秒1个单位长度的速度在线段 上移动,设移动时间为 秒.
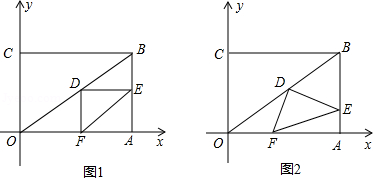
(1)如图1,当 时,求 的长.
(2)如图2,当点 在线段 上移动的过程中, 的大小是否发生变化?如果变化,请说明理由;如果不变,请求出 的值.
(3)连接 ,当 将 分成的两部分的面积之比为 时,求相应的 的值.
如图,在平面直角坐标系中,抛物线 与 轴正半轴交于点 ,且点 的坐标为 ,过点 作垂直于 轴的直线 . 是该抛物线上的任意一点,其横坐标为 ,过点 作 于点 , 是直线 上的一点,其纵坐标为 .以 , 为边作矩形 .
(1)求 的值.
(2)当点 与点 重合时,求 的值.
(3)当矩形 是正方形,且抛物线的顶点在该正方形内部时,求 的值.
(4)当抛物线在矩形 内的部分所对应的函数值 随 的增大而减小时,直接写出 的取值范围.

如图,矩形中,
,
,点
,
分别在边
,
上,点
,
分别在边
,
上,
,
交于点
,记
.
(1)若的值为1,当
时,求
的值.
(2)若的值为
,求
的最大值和最小值.
(3)若的值为3,当点
是矩形的顶点,
,
时,求
的值.

如图,矩形 中,点 为 上一点, 为 的中点,且 .
(1)当 为 中点时,求证: ;
(2)当 时,求 的值;
(3)设 , ,作点 关于 的对称点 ,连接 , ,若点 到 的距离是 ,求 的值.
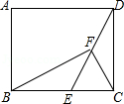
已知在矩形 中,
中, 的平分线
的平分线 与
与 边所在的直线交于点
边所在的直线交于点 ,点
,点 是线段
是线段 上一定点(其中
上一定点(其中
(1)如图1,若点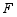 在
在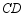 边上(不与
边上(不与 重合),将
重合),将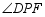 绕点
绕点 逆时针旋转
逆时针旋转 后,角的两边
后,角的两边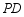 、
、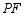 分别交射线
分别交射线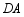 于点
于点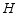 、
、 .
.
①求证: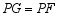 ; ②探究:
; ②探究: 、
、 、
、 之间有怎样的数量关系,并证明你的结论.
之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点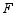 在
在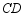 的延长线上(不与
的延长线上(不与 重合),过点
重合),过点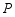 作
作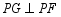 ,交射线
,交射线 于点
于点 ,你认为(1)中
,你认为(1)中 、
、 、
、 之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
如图,矩形OABC的两边OA,OC分别在x轴和y轴的正半轴上,点B的坐标为( ),点D在CB上,且CD:DB=2:1,OB交AD于点E.平行于x轴的直线l从原点O出发,以每秒1个单位长度的速度沿y轴向上平移,到C点时停止;l与线段OB,AD分别相交与M,N两点,以MN为边作等边△MNP(点P在线段MN的下方).设直线l的运动时间为t(秒),△MNP与△OAB重叠部分的面积为S(平分单位).
(1)直接写出点E的坐标;
(2)求S与t的函数关系式;
(3)是否存在某一时刻t,使得 成立?若存在,请求出此时t的值;若不存在,请说明理由.

如图,在平面直角坐标系中,  为原点,四边形
为原点,四边形  是矩形,点
是矩形,点  ,
,  的坐标分别是
的坐标分别是  和
,点
和
,点  是对角线
是对角线  上一动点(不与
上一动点(不与  ,
,  重合),连结
重合),连结  ,作
,作  ,交
,交  轴于点
轴于点  ,以线段
,以线段  ,
,  为邻边作矩形
为邻边作矩形  .
.
(1)填空:点  的坐标为 ;
的坐标为 ;
(2)是否存在这样的点  ,使得
,使得  是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出  的长度;若不存在,请说明理由;
的长度;若不存在,请说明理由;
(3)①求证: ;
②设  ,矩形
,矩形  的面积为
的面积为  ,求
,求  关于
关于  的函数关系式(可利用①的结论),并求出
的函数关系式(可利用①的结论),并求出  的最小值.
的最小值.

如图①,在△ABC中, , , ,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为 时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.

问题提出
(1)如图①,已知直线及
外一点
,试在直线
上确定
、
两点,使
,并画出这个
.
问题探究
(2)如图②,是边长为28的正方形
的对称中心,
是
边上的中点,连接
.试在正方形
的边上确定点
,使线段
和
将正方形
分割成面积之比为
的两部分.求点
到点
的距离.
问题解决
(3)如图③,有一个矩形花园,
,
.根据设计要求,点
、
在对角线
上,且
,并在四边形区域
内种植一种红色花卉,在矩形内其他区域均种植一种黄色花卉.已知种植这种红色花卉每平方米需210元,种植这种黄色花卉每平方米需180元.试求按设计要求,完成这两种花卉的种植至少需费用多少元?(结果保留整数.参考数据:
,

如图:在平面直角坐标系中,直线与
轴交于点
,经过点
的抛物线
的对称轴是
.
(1)求抛物线的解析式;
(2)平移直线经过原点
,得到直线
,点
是直线
上任意一点,
轴于点
,
轴于点
,若点
在线段
上,点
在线段
的延长线上,连接
,
,且
.求证:
;
(3)若(2)中的点坐标为
,点
是
轴上的点,点
是
轴上的点,当
时,抛物线上是否存在点
,使四边形
是矩形?如果存在,请求出点
的坐标,如果不存在,请说明理由.

如图,矩形 的顶点 、 分别位于 轴和 轴的正半轴上,线段 、 的长度满足方程 ,直线 分别与 轴、 轴交于 、 两点,将 沿直线 折叠,点 恰好落在直线 上的点 处,且
(1)求点 的坐标;
(2)求直线 的解析式;
(3)将直线 以每秒1个单位长度的速度沿 轴向下平移,求直线 扫过矩形 的面积 关于运动的时间 的函数关系式.

如图1,在 中,矩形 的一边 在 上,顶点 、 分别在 、 上, 是边 上的高, 交 于点 .若 , , .矩形 恰好为正方形.

(1)求正方形 的边长;
(2)如图2,延长 至 .使得 ,将矩形 沿 的方向向右平移,当点 刚好落在 上时,试判断移动后的矩形与 重叠部分的形状是三角形还是四边形,为什么?
(3)如图3,连接 ,将正方形 绕点 顺时针旋转一定的角度得到正方形 ,正方形 分别与线段 、 相交于点 、 ,求 的周长.
如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒1个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 与矩形 重叠部分的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 的运动过程中,是否存在点 ,使 为等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.

试题篮
()