如图,在平面直角坐标系中,矩形 的边 交 轴于点 , 轴,反比例函数 的图象经过点 ,点 的坐标为 , .
(1)求反比例函数的解析式;
(2)点 为 轴上一动点,当 的值最小时,求出点 的坐标.

如图,点 是矩形 的边 延长线上一点,以 为直径的 交矩形对角
线 于点 ,在线段 上取一点 ,连接 ,使 .
(1)求证: 是 的切线;
(2)若 , , ,求 的长.

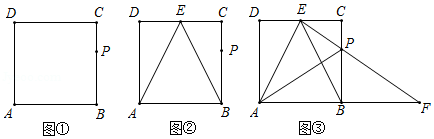
如图1,在 中,矩形 的一边 在 上,顶点 、 分别在 、 上, 是边 上的高, 交 于点 .若 , , .矩形 恰好为正方形.

(1)求正方形 的边长;
(2)如图2,延长 至 .使得 ,将矩形 沿 的方向向右平移,当点 刚好落在 上时,试判断移动后的矩形与 重叠部分的形状是三角形还是四边形,为什么?
(3)如图3,连接 ,将正方形 绕点 顺时针旋转一定的角度得到正方形 ,正方形 分别与线段 、 相交于点 、 ,求 的周长.
如图1,在矩形 中, 是 的中点,以点 为直角顶点的直角三角形 的两边 , 分别过点 , , .

(1)求证: ;
(2)将 绕点 按顺时针方向旋转,当旋转到 与 重合时停止转动,若 , 分别与 , 相交于点 , (如图 .
①求证: ;
②若 ,求 面积的最大值;
③当旋转停止时,点 恰好在 上(如图 ,求 的值.
已知矩形 的一条边 ,将矩形 折叠,使得顶点 落在 边上的 点处
(Ⅰ)如图1,已知折痕与边 交于点 ,连接 、 、 .若 与 的面积比为 ,求边 的长.
(Ⅱ)如图2,在(Ⅰ)的条件下,擦去折痕 、线段 ,连接 .动点 在线段 上(点 与点 、 不重合),动点 在线段 的延长线上,且 ,连接 交 于点 ,作 于点 .试问当动点 、 在移动的过程中,线段 的长度是否发生变化?若变化,说明变化规律.若不变,求出线段 的长度.

如图, 在平面直角坐标系中, 把矩形 沿对角线 所在直线折叠, 点 落在点 处, 与 轴相交于点 ,矩形 的边 , 的长是关于 的一元二次方程 的两个根, 且 .
(1) 求线段 , 的长;
(2) 求证: ,并求出线段 的长;
(3) 直接写出点 的坐标;
(4) 若 是直线 上一个动点, 在坐标平面内是否存在点 ,使以点 , , , 为顶点的四边形是菱形?若存在, 请直接写出 点的坐标;若不存在, 请说明理由 .

如图1,已知矩形 , , ,动点 从点 出发,以 的速度向点 运动,直到点 为止;动点 同时从点 出发,以 的速度向点 运动,与点 同时结束运动.
(1)点 到达终点 的运动时间是 ,此时点 的运动距离是 ;
(2)当运动时间为 时, 、 两点的距离为 ;
(3)请你计算出发多久时,点 和点 之间的距离是 ;
(4)如图2,以点 为坐标原点, 所在直线为 轴, 所在直线为 轴, 长为单位长度建立平面直角坐标系,连接 ,与 相交于点 ,若双曲线 过点 ,问 的值是否会变化?若会变化,说明理由;若不会变化,请求出 的值.

如图,在矩形 中, , , 是 边上的一点,且 .
(1)用尺规在图①中作出 边上的中点 ,连接 、 (保留作图痕迹,不写作法);
(2)如图②,在(1)的条件下,判断 是否平分 ,并说明理由;
(3)如图③,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 ,不添加辅助线, 能否由都经过 点的两次变换与 组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证: ;
(2)若 ,试判断四边形 的形状,并证明你的结论.

如图,在矩形 中, , , 平分 ,分别交 , 的延长线于点 , ;连接 ,过点 作 ,分别交 , 于点 , .
(1)求 的长;
(2)求证: .

试题篮
()