如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是( )
,那么点B′的坐标是( )

| A.(-2,3) | B.(2,-3) |
| C.(3,-2)或(-2,3) | D.(-2,3)或(2,-3) |
(1)知识再现
如图(1):若点A,B在直线l同侧,A,B到l的距离分别是3和2,AB=4,现在直线l上找一点P,使AP+BP的值最小,做法如下;
作点A关于直线l的对称点A′,连接BA′,与直线l的交代就是所求的点P,线段BA′的长度即为AP+BP的最小值,请你求出这个最小值.
(2)实践应用
①如图(2),⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是 ;
②如图(3),Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为 ;
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为 ;
③如图(4),菱形ABCD中AB=2,∠A=120°,点P,Q,K,分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为 ;
④如图(5),在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD= ,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
(3)拓展延伸
如图(6),在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD,保留作图痕迹,不必写出作法.
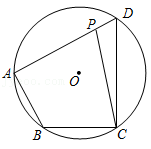
如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为
| A. |
|
B. |
|
C. |
|
D. |
|
某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下:阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.
(1)设一块绿化区的长边为xm,写出工程总造价y与x的函数关系式(写出x的取值范围).
(2)如果小区投资46.9万元,问能否完成工程任务?若能,请写出x为整数的所有工程方案;若不能,请说明理由.(参考值: )
)
如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的坐标为( )

| A.(2,0) | B.( ,0) ,0) |
C.( ,0) ,0) |
D.( ,0) ,0) |
如图,正方向ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 ________ cm.
以下说法错误的是
| A. |
多边形的内角大于任何一个外角 |
| B. |
任意多边形的外角和是 |
| C. |
正六边形是中心对称图形 |
| D. |
圆内接四边形的对角互补 |
下列命题中,正确的是( )
| A.四边相等的四边形是正方形 |
| B.四角相等的四边形是正方形 |
| C.对角线相等的菱形是正方形 |
| D.对角线垂直且相等的四边形是正方形 |
一个多边形的内角和是900°,则这个多边形的边数为( )
| A.6 | B.7 | C.8 | D.9 |
如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,tan∠AEB=3,则GF的长为 .

试题篮
()