如图,□ABCD的对角线AC、BD相交于点O,点E是CD的中点,若AD=4cm,则OE的长为 cm.
如图4,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1 A1、 A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有 个.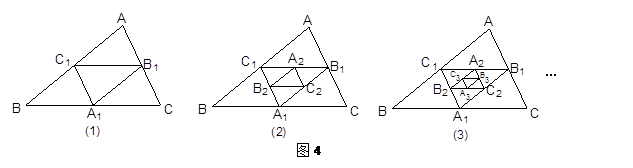
已知:如图,在梯形ABCD中,AD∥BC,∠DCB = 90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当 = 1时,是 ;②当
= 1时,是 ;②当 = 2时,是 ;③当
= 2时,是 ;③当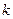 = 3时,是 . 并证明
= 3时,是 . 并证明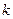 = 2时的结论.
= 2时的结论.
云南 年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形
年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形 (如图
(如图 所示),
所示), ,
, 为水面,点
为水面,点 在
在 上,测得背水坡
上,测得背水坡 的长为
的长为 米,倾角
米,倾角 ,迎水坡
,迎水坡 上线段
上线段 的长为
的长为 米,
米, .
.

(1)请你帮技术员算出水的深度(精确到 米,参考数据
米,参考数据 );
);
(2)就水的深度而言,平均每天水位下降必须控制在多少米以内,才能保证现有水量至少能使用 天?(精确到
天?(精确到 米)
米)
如图6,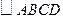 的两条对角线
的两条对角线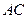 、
、 相交于点
相交于点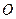 .
.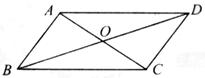
图中有哪些三角形是全等的?
选出其中一对全等三角形进行证明.
如图,直角梯形ABCD中,AB∥DC,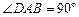 ,
,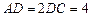 ,
,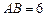 .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当 时,求线段
时,求线段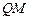 的长;
的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
如图,已知直线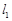 ∥
∥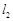 ∥
∥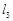 ∥
∥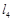 ,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则
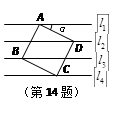
,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则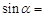 .
.
如图,菱形ABCD由6个腰长为2,且全等的等腰梯形镶嵌而成,则线段AC的长为
| A.3 | B.6 | C. |
D. |
如图,在平面直角坐标系中,梯形ABCD的顶点坐标分别为A ,B
,B ,
, ,D
,D ,将梯形ABCD绕点D逆时针旋转90°得到梯形
,将梯形ABCD绕点D逆时针旋转90°得到梯形 .
.
(1)在平面直角坐标系中画出梯形A1B1C1D,则 的坐标为 ,
的坐标为 , 的坐标为 ,
的坐标为 , 的坐标为 ;
的坐标为 ;
(2)点C旋转到点 的路线长为 (结果保留
的路线长为 (结果保留 ).
).
如图,矩形ABCD中,AB=8cm,BC=4cm,E是DC的中点,BF= BC,则四边形DBFE的面积为
BC,则四边形DBFE的面积为  .
.
(满分11分)
如图,四边形ABCD和四边形AEFG均为正方形,连接BG与DE相交于点H.
(1)证明:△ABG 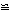 △ADE ;
△ADE ;
(2)试猜想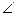 BHD的度数,并说明理由;
BHD的度数,并说明理由;
(3)将图中正方形ABCD绕点A逆时针旋转(0°<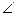 BAE <180°),设△ABE的面积为
BAE <180°),设△ABE的面积为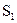 ,△ADG的面积为
,△ADG的面积为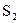 ,判断
,判断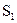 与
与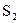 的大小关系,并给予证明.
的大小关系,并给予证明.
如图6,在平行四边形ABCD中,AB = 6cm,∠BCD的平分线交AD于点 ,则线段DE的长度是__________ cm.
,则线段DE的长度是__________ cm.
如图,在平行四边形ABCD中,∠A=130°,在AD上取DE=DC,
则∠ECB的度数是 .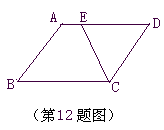
试题篮
()