初中数学圆内接四边形的性质试题

如图，正方形纸片ABCD的边长为8，将其沿EF折叠，

则图中①②③④四个三角形的周长之和为 ▲  ．

如图，在平行四边形ABCD中，CD=10，F是AB边上一点，DF交AC于点E，

且=       ，BF=      .

（本小题满分8分）
　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；
（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

．把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB= 3 cm，BC= 5 cm，则重叠部分△DEF的面积是       cm²．

如图3，

在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是

A．点P

B．点Q

C．点R

D．点M

如图2，在□ABCD中，AC平分∠DAB，AB = 3， 则□ABCD的周长为

A．6

B．9

C．12

D．15

如图，在梯形ABCD中，AB∥CD
（1）用尺规作图方法，作∠DAB的角平分线AF（只保留作图痕迹，不写作法和证明）
（2）若AF交CD边于点E，判断△ADE的形状（只写结果）

如图，P是菱形ABCD对角线BD上一点，PE⊥AB于点E，PE＝4cm，

则点P到BC的距离是_____cm.

如图，在梯形ABCD中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB＝30°.点E、F同时从B点出发，沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG．设E点移动距离为x（x＞0）.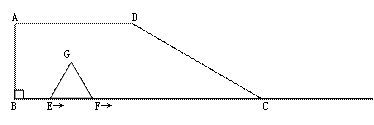

⑴△EFG的边长是____（用含有x的代数式表示），当x＝2时，点G的位置在_______；
⑵若△EFG与梯形ABCD重叠部分面积是y，求
①当0＜x≤2时，y与x之间的函数关系式；
②当2＜x≤6时，y与x之间的函数关系式；
⑶探求⑵中得到的函数y在x取含何值时，存在最大值，并求出最大值.

如图4，等腰梯形ABCD中，AD∥BC，AB=DC=5，中位线EF的长为6，则这个等腰梯形的周长为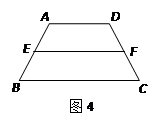

A．11

B．16

C．17

D．22

如图3，矩形内两相邻正方形的面积分别是2和6，那么矩形内阴影部分的面积是

A．2-2

B．3-2

C．2-1

D．6-2

如图2，将△ABC沿DE翻折，折痕DE∥BC，若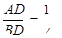，BC=6，则DE长等于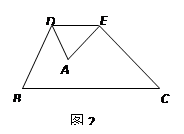

A．1.8

B．2

C．2.5

D．3

．(10分)如图9，正方形ABCD边长为10cm，P、Q分别是BC、CD上的两个动点，当P 点在BC上运动时，且A P⊥PQ.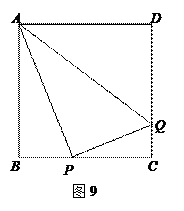

（1）求证：△ABP∽△PCQ；
（2）当BP等于多少时，四边形ABCQ的面积为62cm²．

如图7，一个农户用24m长的篱笆围成一排一面靠墙、大小相等且彼此相连的三个矩形鸡舍.

要使这三个鸡舍的总面积为36m²，求每个鸡舍的长和宽各是多少.

观察图2，利用图形间的面积关系，写出一个代数恒等式：                   .