初中数学圆内接四边形的性质选择题

如图，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD延长线于点F，则△EDF与△BCF的周长之比是（ ）

A．1：2

B．1：3

C．1：4

D．1：5

平行四边形ABCD的周长32，5AB=3BC，则对角线AC的取值范围为（ ）

A．6＜AC＜10

B．6＜AC＜16

C．10＜AC＜16

D．4＜AC＜16

顺次连接矩形ABCD各边中点，所得四边形必定是（ ）

A．邻边不等的平行四边形	B．矩形
C．正方形	D．菱形

下列命题正确的是（ ）

A．一组对边平行，另一组对边相等的四边形是平行四边形

B．对角线互相垂直的四边形是菱形

C．对角线相等的四边形是矩形

D．一组邻边相等的矩形是正方形

如图，两个边长为1cm的正方形一个顶点在另一个的中心，则重合部分（阴影部分）的面
积为（    ）

A．

B．

C．

D．不能确定

如图，四边形ABCD，已知AC=BD，E、F、G、H 分别是边AB、BC、CD、DA的中点，
连接EF、FG、GH、HE，四边形EFGH一定是（ ）

（A）正方形                   （B）矩形
（C）菱形                     （D）平行四边形

如图是由4个边长为1的正方的平行四边形的个数是形构成的网格．用没有刻度的直尺在这个网格中最多可以作出一组对边长度为的平行四边形的个数是（ ）

A．2个

B．4个

C．6个

D．8个

如图，在正方形ABCD的外面，作等边三角形DCE，则∠AED的度数为（ ）

A．10°

B．20°

C．15°

D．30°

菱形的两条对角线长分别为18与24，则此菱形的周长为（ ）

A．15

B．30

C．60

D．120

平行四边形的一个内角为40°，它的另一个内角等于（ ）

A．40°

B．140°

C．40°或140°

D．50°

如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=5，AD=12，则四边形ABOM的周长为（   ）

A．17

B．18

C．19

D．20

如图所示，在▱ABCD中，对角线AC，BD相交于点O，E，F是对角线AC上的两点，当E，F满足下列哪个条件时，四边形DEBF不一定是平行四边形（ ）

A．OE="OF"

B．DE="BF"

C．∠ADE="∠CBF"

D．∠ABE=∠CDF

如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（ ）

A．矩形 B.菱形 C.正方形 D.等腰梯形

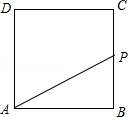
如图，正方形ABCD的边长为4，P为正方形边上一动点，沿A→D→C→B→A 的路径匀速移动，设P点经过的路径长为x，△APD的面积是y，则下列图象能大致反映y与x的函数关系的是（ ）

A．	B．
C．	D．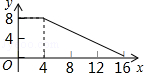

如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论：（1）AE=BF；（2）AE⊥BF；（3）AO=OE；（4）S_△AOB=S_{四边形DEOF}中正确的有（ ）

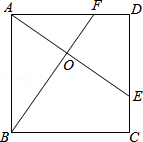
A. 4个 B.3个   C.2个 D.1个