初中数学圆内接四边形的性质选择题

在矩形ABCD中，AD=3AB，点G、H分别在AD、BC上，连BG、DH，且BG∥DH，当=（ ）时，四边形BHDG为菱形．

A. B. C. D.

从多边形一个顶点出发的对角线把多边形分得2003个三角形，则这个多边形的边数为（   ）．

A．2001

B．2005

C．2004

D．2006

下列四个命题，其中真命题是（   ）

A．方程的解是

B．3的平方根是

C．有两边和一个角分别对应相等的两个三角形全等

D．连接任意四边形各边中点的四边形是平行四边形

如图，E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（   ）．

A．一组对边平行而另一组对边不平行

B．对角线相等

C．对角线互相垂直

D．对角线互相平分

下列命题是假命题的是（ ）

A．不在同一直线上的三点确定一个圆

B．正六边形的内角和是720°

C．矩形的对角线互相垂直且平分

D．角平分线上的点到角两边的距离相等

如图， $\odot O$ 中，点 $C$ 为弦 $\mathit{AB}$ 中点，连接 $\mathit{OC}$ ， $\mathit{OB}$ ， $\angle \mathit{COB}=56°$ ，点 $D$ 是 $\stackrel{̂}{\mathit{AB}}$ 上任意一点，则 $\angle \mathit{ADB}$ 度数为 $($ 　　 $)$

A．

$112°$

B．

$124°$

C．

$122°$

D．

$134°$

如图，图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AH＞HB，判断三人行进路线长度的大小关系为（ ）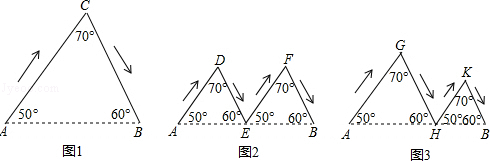

A．甲＜乙＜丙	B．乙＜丙＜甲
C．丙＜乙＜甲	D．甲=乙=丙

如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则等于（ ）
    
A．           B．         C．         D．

如图，四边形 $\mathit{ABCD}$ 内接于 $\odot O$ ，若 $\angle A=80°$ ，则 $\angle C$ 的度数是 $($ 　　 $)$

A．

$80°$

B．

$100°$

C．

$110°$

D．

$120°$

如图，四边形 $\mathit{ABCD}$ 是 $\odot O$ 的内接四边形， $\angle B=90°$ ， $\angle \mathit{BCD}=120°$ ， $\mathit{AB}=2$ ， $\mathit{CD}=1$ ，则 $\mathit{AD}$ 的长为 $($ 　　 $)$

A．

$2\sqrt{3}-2$

B．

$3-\sqrt{3}$

C．

$4-\sqrt{3}$

D．

2

如图，已知四边形 $\mathit{ABCD}$内接于 $\odot O$， $\angle \mathit{ABC}=70°$，则 $\angle \mathit{ADC}$的度数是 $($　　 $)$

A． $70°$B． $110°$C． $130°$D． $140°$

如图，四边形 $\mathit{ABCD}$的外接圆为 $\odot O$， $\mathit{BC}=\mathit{CD}$， $\angle \mathit{DAC}=35°$， $\angle \mathit{ACD}=45°$，则 $\angle \mathit{ADB}$的度数为 $($　　 $)$

A． $55°$B． $60°$C． $65°$D． $70°$

如图，四边形 内接于 ， ， ，则 的大小为 　　

A．

B．

C．

D．

如图，矩形ABCD中，AB=12cm，BC=24cm，如果将该矩形沿对角线BD折叠，那么图中阴影部分的面积（ ）cm²．

A．72

B．90

C．108

D．144

顺次连接等腰梯形四边中点得到一个四边形，再顺次连接所得四边形的中点得到的图形是 （   ）

A．等腰梯形

B．菱形

C．直角梯形

D．矩形