如图,在平行四边形ABCD中,AC、BD相交于点O,点E、F分别是OB、OD的中点.判断四边形AECF的形状并说明理由.
(本小题满分10分)如图,在四边形ABCD中,AD∥BC,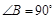 ,AD=8cm,BC=10cm,
,AD=8cm,BC=10cm,
AB=6cm,,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向点C运动,P、Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(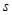 ).
).
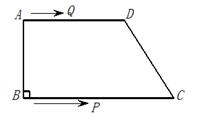
(1)直接写出:QD= ,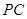 = ;(用含t的式子表示)
= ;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当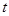 为何值时,
为何值时, 是等腰三角形?
是等腰三角形?
如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
(1)若AB=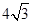 ,求
,求 的长;(结果保留π)
的长;(结果保留π)
(2)求证:四边形ABMC是菱形.
如图,在平行四边形ABCD中,AC是它的一条对角线,BE⊥AC于点E,DF⊥AC于点F,求证:四边形BEDF是平行四边形.
(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.

(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
(本小题9分)如图,P是正方形ABCD内一点,连接PA、PB、PC,将△ABP绕点B顺时针旋转到△CBP′的位置.
(1)旋转中心是点 ______,点P旋转的度数是______;
(2)连接PP′,△BPP′的形状是 ______三角形;
(3)若PA=2,PB=4,∠APB=135°.
①求△BPP′的周长; ②求PC的长.
如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.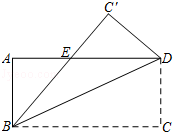
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
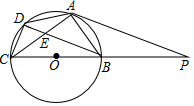
如图,四边形 内接于 , 为 的直径, 与 交于点 , 为 延长线上一点,连接 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 长;
(3)在(2)的条件下,若 ,求 的面积.
已知关于 的一元二次方程
的一元二次方程 的两个实数根
的两个实数根 、
、 的值分别是□ABCD的两边AB、AD的长.
的值分别是□ABCD的两边AB、AD的长.
(1)如果 ,试求□ABCD的周长;
,试求□ABCD的周长;
(2)当 为何值时,□ABCD是菱形?
为何值时,□ABCD是菱形?
如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.
(1)求证:△BEC≌△DFA;
(2)求证:四边形AECF是平行四边形.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE,两线交于点F.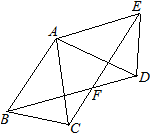
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.
试题篮
()