如图,已知等腰梯形ABCD,AD∥BC,∠D=120°
(1)用直尺和圆规作出∠BAD的平分线AE,交BC于点 ,(保留作图痕迹,不要求写作法);
,(保留作图痕迹,不要求写作法);
(2)求证:四边形AECD是平行四边形。
如图,在Rt△ABC中,∠C=90°,O是斜边AB上的中点,AE=CE,BF∥AC.
(1)求证:△AOE≌△BOF;
(2)求证:四边形BCEF是矩形.
写出下列命题的已知、求证,并完成证明过程.
命题:如果平行四边形的一条对角线平分它的一个内角,那么这个平行四边形是菱形.
已知:如图, .
求证: .
证明:
已知矩形ABCD的周长为12,E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y.
(1)请直接写出y与x的函数关系式;
(2)根据(1)中的函数关系式,计算当x为何值时,y最大,并求出最大值.
(参考公式:当x=- 时,二次函数y=ax+bx+c(a≠o)有最小(大)值
时,二次函数y=ax+bx+c(a≠o)有最小(大)值 )
)
两组邻边分别相等的四边形我们称它为筝形.
如图,在筝形 中,
中, ,
, ,
, ,
, 相交于点
相交于点 ,
,
(1)求证:① ;
;
② ,
, ;
;
(2)如果 ,
, ,求筝形
,求筝形 的面积.
的面积.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
(1)求证:CD=AN;
(2)若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
如图,已知△ABC,按如下步骤作图:①分别以A、C为圆心,以大于 的长为半径在AC两边作弧,交于两点M、N;②作直线MN,分别交AB、AC于点D、O;③过C作CE∥AB交MN于点E,连接AE、CD.
的长为半径在AC两边作弧,交于两点M、N;②作直线MN,分别交AB、AC于点D、O;③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形;
(2)当∠ACB 90°,BC
90°,BC 6,AB
6,AB 10,求四边形ADCE的面积.
10,求四边形ADCE的面积.
如图,在矩形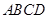 中,对角线
中,对角线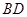 的垂直平分线
的垂直平分线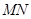 与
与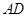 相交于点
相交于点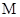 ,与
,与 相较于点
相较于点 ,与
,与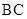 相较于
相较于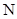 ,连接
,连接 .请你判定四边形
.请你判定四边形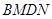 是什么特殊四边形,并说明理由.
是什么特殊四边形,并说明理由.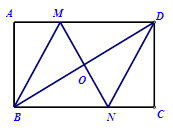
在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
【感知】如图1,当点H与点C重合时,可得FG=FD.
【探究】如图2,当点H为边CD上任意一点时,猜想FG与FD的数量关系,并说明理由.
【应用】在图2中,当AB=5,BE=3时,利用探究结论,求FG的长.
如图,已知在□ABCD中,AB⊥AC,AB=OA,BC= ,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点EF.
,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点EF.
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试证明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,说明理由并求出此时AC绕点O顺时针旋转的度数.
如图,在菱形ABCD中,∠A=60°, =4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1)求∠ABD 的度数;
(2)求线段 的长.
的长.
试题篮
()