初中数学圆内接四边形的性质解答题

已知：在四边形中，是边的中点，、互相平分并交于点O，求证：四边形是平行四边形．

（本题6分）如图，正方形BCD中，点E，F分别在AB，BC上，AF=DE，AF和DE相交于点G

（1）观察图形，写出图中所有与∠AED相等的角；
（2）选择图中与∠AED相等的任意一个角，并加以证明。

如图，将□ABCD沿过点A的直线折叠，使点D落到AB边上的点处，折痕交CD边于点E，连接BE

（1）求证：四边形是平行四边形
（2）若BE平分∠ABC，求证：

如图，在四边形ABCD中，AB=CD，BE=DF；AE⊥BD，CF⊥BD，对角线AC、BD相交于点O，
求证：AO=CO．

（1）已知：如图1，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．
（2）如图2，AB切⊙O于点B，OA=2，∠OAB=30°，弦BC∥OA．求：劣弧BC的长．（结果保留π）

（本小题满分6分）已知：如图，，是□ABCD的对角线上的两点，，求证：．

求证：平行四边形的对角线互相平分（要求：根据题意先画出图形并写出已知、求证、再写出证明过程）．

在平行四边形ABCD中，将△BCD沿BD翻折，使点C落在点E处，BE和AD相交于点O，求证：OA=OE．

如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A₁C₁D₁．

（1）证明：△A₁AD₁≌△CC₁B；
（2）若∠ACB=30°，试问当点C₁在线段AC上的什么位置时，四边形ABC₁D₁是菱形．（直接写出答案）

如图，菱形ABCD中，对角线AC、BD交于O点，DE∥AC，CE∥BD．

（1）求证：四边形OCED为矩形；
（2）在BC上截取CF＝CO，连接OF，若AC＝16，BD＝12，求四边形OFCD的面积．

如图，CD是∠ECB的平分线，∠ECB=50°，∠B=70°，DE∥BC，求∠EDC和∠BDC的度数．

（本题12分）正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A按顺时针方向旋转，记旋转角∠DAG=α，其中0°≤α≤180°，连结DF，BF，如图。

（1）若α=0°，则DF=BF，请加以证明；
（2）试画一个图形（即反例），说明（1）中命题的逆命题是假命题；
（3）对于（1）中命题的逆命题，如果能补充一个条件后能使该逆命题为真命题，请直接写出你认为需要补充的一个条件，不必说明理由。

如图：在平行四边形ABCD中，点E在BA的延长线上，且：BE=AD，点F在AD上，AF=AB
求证：CF=EF

如图，已知⊙O为△ABC的外接圆，BC为直径，点E在AB上，过点E作EF⊥BC，点G在FE的延长线上，且GA=GE．

（1）求证：AG与⊙O相切；
（2）若AC=6，AB=8，BE=3，求线段OE的长．

（本小题满分8分）已知：如图，在平行四边形ABCD中，点M在边AD上，且AM=DM．CM、BA的延长线相交于点E．求证：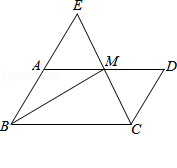

（1）AE=AB；
（2）如果BM平分∠ABC，求证：BM⊥CE．