初中数学圆内接四边形的性质解答题

在图1至图3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．

如图1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，
求证：FM = MH，FM⊥MH
将图-1中的CE绕点C顺时针旋转一个锐角，得到图2，
求证：△FMH是等腰直角三角形
将图2中的CE缩短到图3的情况，△FMH还是等腰直角三角形吗？（不必
说明理由）

如图①，在正方形ABCD中，点E、F分别为边BC、CD的中点，AF、DE相交于点G，则可得结论：①AF=DE，②AF⊥DE。(不需要证明)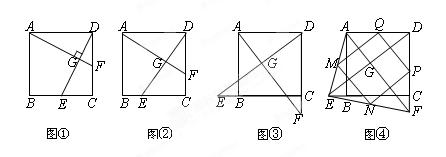

如图②，若点E、F不是正方形ABCD的边BC、CD的中点，但满足CE=DF。则上面的结论①、②是否仍然成立？(请直接回答“成立”或“不成立”)
如图③，若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论①、②是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由。
如图④，在(2)的基础上，连接AE和EF，若点M、N、P、Q分别为AE、EF、FD、AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种？并写出证明过程。

如图，□ABCD的周长是36，且AB∶BC＝5∶4，对角线AC、BD相交于点O，且BD⊥AD，求OB的长。

如图，将矩形纸片沿对角线折叠，点落在点处，交于点，连结．求证：

如图，在△ABC中，O是AC上的一个动点（不与点A、C重合），过O点作直线MN//BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。

（1）试说明：OE=OF。
（2）当O点运动到何处时，四边形AECF是矩形？并证明你的结论。

如图，四边形ABCD中，AB∥CD，AC平分∠BAD ，CE∥AD交AB于点E。

判断：四边形AECD是什么形状？并给出理由。
若点E是AB的中点，是判断△ABC的形状，并给出理由。

如图，在长方形ABCD中，，AB=6cm，BC=8cm，按图中所示方法将△BCD沿BD折叠，使点C落在点E处，BE交AD于点F，

求证：△FBD是等腰三角形；
求AF长。

如图，世博园段的浦江两岸互相平行，C、D是浦西江边间隔200m的两个场馆．海宝在浦东江边的宝钢大舞台处，测得，然后沿江边走了500m到达世博文化中心处，测得，求世博园段黄浦江的宽度(结果可保留根号)．

如图，在矩形ABCD中，AB=3cm，AD=4cm，点E是BC上一动点（不与B、C重合），且DF⊥AE，垂足为F. 设AE=xcm，DF=ycm.
（1）求证：△DFA∽△ABE；
（2）试求y与x之间的函数关系式，并求出自变量的取值范围.

在四边形ABCD中，AD∥BC，且AD＞BC，BC=6cm，P、Q分别从A、C
同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C出发向B运动，几
秒后四边形ABQP是平行四边形？

如图，在梯形ABCD中，AD∥BC，AB=AD+BC，E为CD的中点.
求证：AE⊥BE.

已知口ABCD中，M是边AB的中点，且BM=CM试说明四边形ABCD是矩形

已知正方形ABCD的边长是2，E是CD的中点，动点P从点A出发，沿A→B→C→E运动，到达E点即停止运动，若点P经过的路程为x，△APE的面积记为y，试求出y与x之间的函数解析式，并求出当y＝时，x的值．

如图，D,E分别是△ABC的AB,AC边上的点，且DE∥BC,已知AD︰DB=1︰3, DE=2cm,
求BC的长.
若△ADE的面积为1.5cm²，求梯形DBCE的面积.

已知如图，矩形OABC的长OA=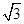，宽OC=1，                         
将△AOC沿AC翻折得△APC.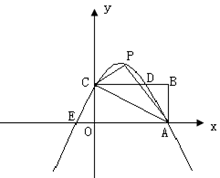

求∠PCB的度数
若P，A两点在抛物线y=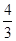－x²+bx+c上，求b，c的值，并                          说明点C在此抛物线上；
（2）中的抛物线与矩形OABC边CB相交于点D，与x轴相交                         于另外一点E，若点M是x轴上的点，N是y轴上的点，以点E、M、D、N为顶点的四边形是平行四边形，试求点M、N的坐标.