在平面直角坐标系xOy中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于F.
(1)求OA,OC的长;
(2)求证:DF为⊙O′的切线;
(3)由已知可得,△AOE是等腰三角形.那么在直线BC上是否存在除点E以外的点P,使△AOP也是等腰三角形?如果存在,请你证明点P与⊙O′的位置关系,如果不存在,请说明理由.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
如图,△ ABC内接于⊙ O, BC=2, AB= AC,点 D为 上的动点,且cos∠ ABC= .
(1)求 AB的长度;
(2)在点 D的运动过程中,弦 AD的延长线交 BC延长线于点 E,问 AD• AE的值是否变化?若不变,请求出 AD• AE的值;若变化,请说明理由;
(3)在点 D的运动过程中,过 A点作 AH⊥ BD,求证: BH= CD+ DH.

如图,将长方形纸片ABCD沿着EF折叠,使得点C与点A重合.
(1)求证:AE=AF;
(2)若AB=3,BC=9,试求CF的长;
(3)在(2)的条件下,试求EF的长.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8)、动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动、其中,点M沿OA向终点A运动,点N沿BC向终点C运动、过点N作NP⊥BC,交AC于P,连结MP、已知动点运动了t秒、

(1)P点的坐标为( , )(用含t的代数式表示);
(2)试求△MPA面积的最大值,并求此时t的值;
(3)请你探索:当t为何值时,△MPA是一个等腰三角形?
如图,长方形ABCO的顶点A、C、O都在坐标轴上,点B的坐标为(8,3),M为AB的中点.
(1)试求点M的坐标和△AOM的周长;
(2)若P是OC上的一个动点,它以每秒1个单位长度的速度从点C出发沿射线CO方向匀速运动,设运动时间为t秒(t>0).
①若△POM的面积等于△AOM的面积的一半,试求t的值;
②是否存在某一时刻t,使△POM是等腰三角形?若存在,求出此时t的值;若不存在,试说明理由.
如图,四边形 内接于圆, ,对角线 平分 .
(1)求证: 是等边三角形;
(2)过点 作 交 的延长线于点 ,若 , ,求 的面积.

如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF.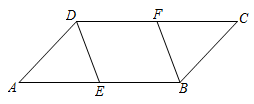
求证:△ADE≌△CBF.
如图:AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于D,DE⊥OC,垂足为E。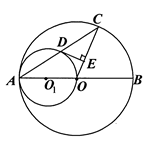
(1)求证:AD=DC
(2)求证:DE是的切线
(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论。
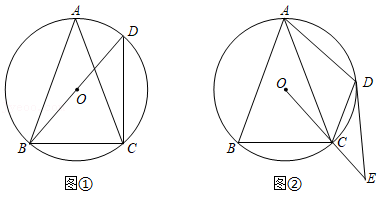
已知 内接于 , , ,点 是 上一点.
(Ⅰ)如图①,若 为 的直径,连接 ,求 和 的大小;
(Ⅱ)如图②,若 ,连接 ,过点作 的切线,与 的延长线交于点 ,求 的大小.
如图,四边形 内接于 , ,延长 到点 ,使得 ,连接 .
(1)求证: ;
(2)若 , , ,求 的值.

如图,在以线段 为直径的 上取一点 ,连接 、 .将 沿 翻折后得到 .
(1)试说明点 在 上;
(2)在线段 的延长线上取一点 ,使 .求证: 为 的切线;
(3)在(2)的条件下,分别延长线段 、 相交于点 ,若 , ,求线段 的长.

如图,在 中, ,以 为直径的 与边 , 分别交于 , 两点,过点 作 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)求证: 为 的中点;
(3)若 , ,求 的长.

如图,在中,
,
是
上一点,
经过点
、
、
,交
于点
,过点
作
,交
于点
.
求证:(1)四边形是平行四边形;
(2).

试题篮
()