初中数学圆内接四边形的性质填空题

如图，在3×3的正方形网格中标出了∠1和∠2．则∠1+∠2=      ．

如图，正方形ABCD的面积为16，点F在AD上，点E在AB的延长线上，FC⊥CE，△CEF的面积为12.5，则BE的值为      ．

如图，在△ABC中，点D、E、F分别在边AB，BC，CA上，且DE∥CA，DF∥BA．下列四种说法：
①四边形AEDF是平行四边形；
②如果∠BAC=90°，那么四边形AEDF是矩形；
③如果AD平分∠BAC，那么四边形AEDF是菱形；
④如果AD⊥BC且AB=AC，那么四边形AEDF是菱形．
其中，正确的有              （只填写序号）．

如图，菱形ABCD的边长为4，过点A，C作对角线AC的垂线，分别交CB和AD的延长线于点E，F，AE=3，则四边形AECF的周长为          ．

如图，已知P是正方形ABCD对角线BD上一点，且BP=BC，则∠ACP度数是      度．

已知菱形的两条对角线长分别为2cm，3cm，则它的面积是         cm²．

如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（ ）

A．①②

B．②③

C．①③

D．①④

如图，正方形ABCD中，点E、F分别在AB、BC上，DH⊥EF于H，DA=HD，EH=2，HF=3．则正方形ABCD的边长为         ．

顺次连接矩形四条边的中点，所得到的四边形一定是        形．

设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的圆的圆心O在直线l上运动，A、O两点之间的距离为d．
（1）如图①，当r＜a时，填表：

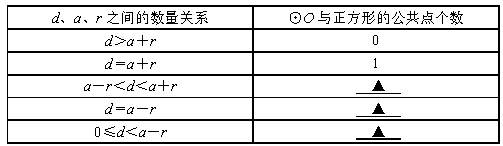
（2）如图②，⊙O与正方形有5个公共点B、C、D、E、F，求此时r与a之间的数量关系；

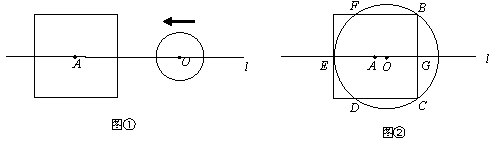
（3）由（1）可知，d、a、r之间的数量关系和⊙O与正方形的公共点个数密切相关．当r=a时，请根据d、a、r之间的数量关系，判断⊙O与正方形的公共点个数；
（4）当r与a之间满足（2）中的数量关系时，⊙O与正方形的公共点个数为    ．

如图，矩形中，,点是边上一点，连接，把沿折叠，使点落在点处，当△为直角三角形时，的长为              

有下列4个命题：①方程x²﹣（+）x+=0的根是和．②在△ABC中，∠ACB=90°，CD⊥AB于D．若AD=4，BD=，则CD=3．③点P（x，y）的坐标x，y满足x²+y²+2x﹣2y+2=0，且xy=k，则k=﹣1．④如图，折叠矩形纸片ABCD，使B点落在AD上一点E处，折痕的两端点分别在AB、BC上（含端点），且AB=6，BC=10。设AE=x，则x 的取值范围是2≤x≤6．上述4个命题中，真命题的序号是                 ．

如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如果大正方形的面积是13，小正方形的面积是1，那么每个直角三角形的周长为          ．

已知：四边形ABED中，AD⊥DE、BE⊥DE．
（1）如图1，点C是边DE的中点，且AB=2AD=2BE．判断△ABC的形状：          （不必说明理由）；
（2）保持图1中△ABC固定不变，将直线DE绕点C旋转到图2中所在的MN的位置（垂线段AD、BE在直线MN的同侧）．试探究线段AD、BE、DE长度之间有什么关系？并给予证明；
（3）保持图2中△ABC固定不变，继续绕点C旋转DE所在的直线MN到图3中的位置（垂线段AD、BE在直线MN的异侧）．⑵中结论是否依然成立，若成立请证明；若不成立，请写出新的结论，并给予证明．

 

有两块同样大小且含角60°的三角板，把它们相等的边拼在一起（两块三角板不重叠），可以拼出            个四边形．