如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数 (x>0)的图象经过BC边上的中点D,交AB于点E.
(x>0)的图象经过BC边上的中点D,交AB于点E.
(1)k的值为_________;
(2)猜想△OCD的面积与△OBE的面积之间的关系,请说明理由.
如图, 是 的中线, 是线段 上一点(不与点 重合). 交 于点 , ,连接 .
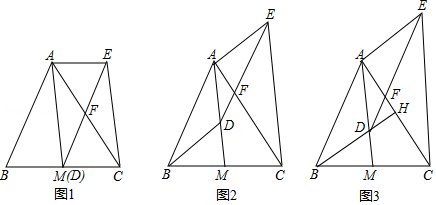
(1)如图1,当点 与 重合时,求证:四边形 是平行四边形;
(2)如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 交 于点 ,若 ,且 .
①求 的度数;
②当 , 时,求 的长.
如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数 在第一象限内的图象与△ABC有交点,则k的取值范围是( )
在第一象限内的图象与△ABC有交点,则k的取值范围是( )

A.2≤k≤ |
B.6≤k≤10 | C.2≤k≤6 | D.2≤k≤ |
如图所示,在平面内有一线段AB,分别过A点,B点向x轴作垂线,垂足分别为C、D,我们把线段CD称之为线段AB在x轴上的射影,线段CD的长称之为线段AB在x轴上的射影长.
(1)双曲线 上有两点A、B,A(m,4),B(n,1),求AB在x轴上的射影长;
上有两点A、B,A(m,4),B(n,1),求AB在x轴上的射影长;
(2)直线 的图象上有两点A、B,AB在x轴上的射影长为4,求AB的长;
的图象上有两点A、B,AB在x轴上的射影长为4,求AB的长;
(3)已知抛物线 和直线
和直线 ,其中
,其中 、
、 、
、 满足
满足 ,抛物线过点(1,0),且与直线相交于A、B两点,求线段AB在x轴上的射影长CD的取值范围.
,抛物线过点(1,0),且与直线相交于A、B两点,求线段AB在x轴上的射影长CD的取值范围.
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .
,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .

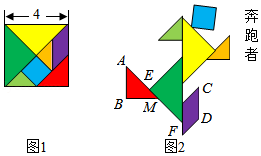
小丽在"红色研学"活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的"奔跑者"形象来激励自己.已知图1正方形纸片的边长为4,图2中 ,则"奔跑者"两脚之间的跨度,即 , 之间的距离是 .
如图,在 中, , , ,以点 为圆心,2为半径的圆与 交于点 ,过点 作 交 于点 ,点 是边 上的动点.当 最小时, 的长为
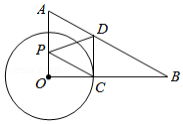
A. B. C.1D.
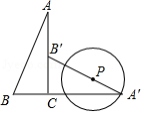
如图, 中, , , ,将 绕点 顺时针旋转 得到△ , 为线段 上的动点, 以点 为圆心, 长为半径作 ,当 与 的边相切时, 的半径为 .
如图,四边形 中, , , , , 为 的中点, 为线段 上的点,且 ,则点 到边 的距离是
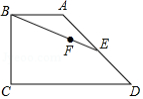
A.3B. C.4D.
如图, 的面积为 .点 , , , , 是边 的 等分点 ,且 为整数),点 , 分别在边 , 上,且 ,连接 , , , , ,连接 , , , , ,线段 与 相交于点 ,线段 与 相交于点 ,线段 与 相交于点 , ,线段 与 相交于点 ,则△ ,△ ,△ , ,△ 的面积和是 .(用含有 与 的式子表示)

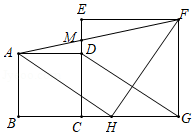
如图,正方形的边
在正方形
的边
上,连接
,过点
作
,交
于点
.连接
,
,其中
交
于点
.
(1)求证:为等腰直角三角形.
(2)若,
,求
的长.
试题篮
()