如图,已知正比例函数与反比例函数交于A(-1,2),B(1,-2)两点,当正比例函数的值大于反比例函数值时,x的取值范围为____________________.
(1)如图1,是正方形
边
上的一点,连接
、
,将
绕点
逆时针旋转
,旋转后角的两边分别与射线
交于点
和点
.
①线段和
的数量关系是 ;
②写出线段,
和
之间的数量关系.
(2)当四边形为菱形,
,点
是菱形
边
所在直线上的一点,连接
、
,将
绕点
逆时针旋转
,旋转后角的两边分别与射线
交于点
和点
.
①如图2,点在线段
上时,请探究线段
、
和
之间的数量关系,写出结论并给出证明;
②如图3,点在线段
的延长线上时,
交射线
于点
,若
,
,直接写出线段
的长度.

如图,已知反比例函数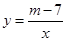 的图象的一支位于第一象限.
的图象的一支位于第一象限.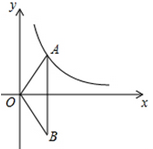
(1)求m的取值范围;
(2)O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
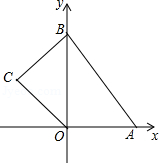
如图,在平面直角坐标系中,四边形 的顶点 是坐标原点,点 的坐标为 ,点 的坐标为 ,点 的坐标为 , ,点 , 分别为四边形 边上的动点,动点 从点 开始,以每秒1个单位长度的速度沿 路线向终点 匀速运动,动点 从 点开始,以每秒两个单位长度的速度沿 路线向终点 匀速运动,点 , 同时从 点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间 秒 , 的面积为 .
(1)填空: 的长是 , 的长是 ;
(2)当 时,求 的值;
(3)当 时,设点 的纵坐标为 ,求 与 的函数关系式;
(4)若 ,请直接写出此时 的值.
李明同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y,这样就确定点P的一个坐标( ,
, ),那么点P落在双曲线
),那么点P落在双曲线 上的概率为( )
上的概率为( )
A. |
B. |
C. |
D. |
如图,反比例函数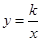 (k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,
(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,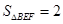 ,则k的值为 .
,则k的值为 .
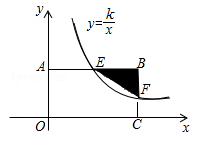
小丽在"红色研学"活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的"奔跑者"形象来激励自己.已知图1正方形纸片的边长为4,图2中 ,则"奔跑者"两脚之间的跨度,即 , 之间的距离是 .
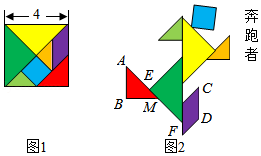
如图,在 中, , , ,以点 为圆心,2为半径的圆与 交于点 ,过点 作 交 于点 ,点 是边 上的动点.当 最小时, 的长为
A. B. C.1D.
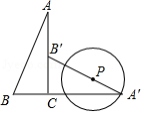
如图, 中, , , ,将 绕点 顺时针旋转 得到△ , 为线段 上的动点, 以点 为圆心, 长为半径作 ,当 与 的边相切时, 的半径为 .
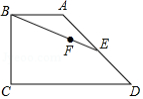
如图,四边形 中, , , , , 为 的中点, 为线段 上的点,且 ,则点 到边 的距离是
A.3B. C.4D.
如图, 的面积为 .点 , , , , 是边 的 等分点 ,且 为整数),点 , 分别在边 , 上,且 ,连接 , , , , ,连接 , , , , ,线段 与 相交于点 ,线段 与 相交于点 ,线段 与 相交于点 , ,线段 与 相交于点 ,则△ ,△ ,△ , ,△ 的面积和是 .(用含有 与 的式子表示)

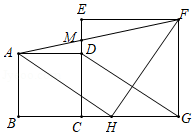
如图,正方形的边
在正方形
的边
上,连接
,过点
作
,交
于点
.连接
,
,其中
交
于点
.
(1)求证:为等腰直角三角形.
(2)若,
,求
的长.
试题篮
()