如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2﹣18x+72=0的两根(OA>OC),BE=5,tan∠ABO=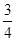 .
.
(1)求点A,C的坐标;
(2)若反比例函数y= 的图象经过点E,求k的值;
的图象经过点E,求k的值;
(3)若点P在坐标轴上,在平面内是否存在一点Q,使以点C,E,P,Q为顶点的四边形是矩形?若存在,请写出满足条件的点Q的个数,并直接写出位于x轴下方的点Q的坐标;若不存在,请说明理由.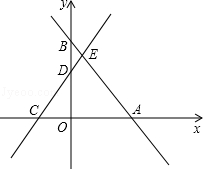
(黄石)已知双曲线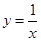 (
(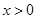 ),直线
),直线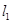 :
: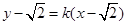 (
(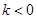 k<0)过定点F且与双曲线交于A,B两点,设A(
k<0)过定点F且与双曲线交于A,B两点,设A(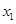 ,
,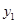 ),B(
),B(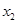 ,
, )(
)(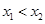 ),直线
),直线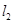 :
: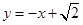 .
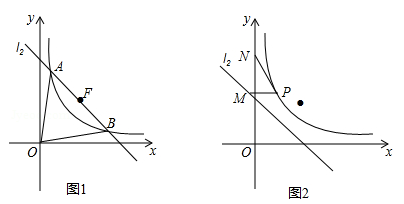
.
(1)若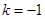 ,求△OAB的面积S;
,求△OAB的面积S;
(2)若AB=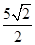 ,求k的值;
,求k的值;
(3)设N(0,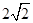 ),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(
),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(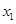 ,
,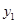 ),B(
),B(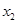 ,
, )则A,B两点间的距离为AB=
)则A,B两点间的距离为AB=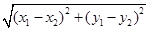 .
.
如图,直线x=t(t>0)与反比例函数y=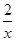 ,y=
,y=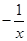 的图象分别交于B,C两点,A为y 轴上的任意一点,则△ABC的面积为( )
的图象分别交于B,C两点,A为y 轴上的任意一点,则△ABC的面积为( )
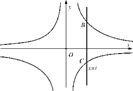
| A.3 | B.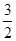 t t |
C.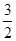 |
D.不能确定 |
六•一儿童节,小文到公园游玩,看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等,比如:A、B、C是弯道MN上任三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等. 爱好数学的他建立了平面直角坐标系(如图).图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米),OG=GH=HI.
(1)求S1和S3的值;
(2)设T 是弯道MN上的任一点,写出y关于x的函数关系式;
是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改选,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、D两点,与反比例函数y=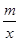 的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0, -6)且S△DBP=27.
的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0, -6)且S△DBP=27.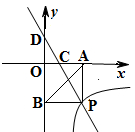
(1)求上述一次函数与反比例函数的表达式;
(2)设点Q是一次函数y=kx+3图象上的一点,且满足S△DOQ="2" S△COD,求点Q的坐标.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求过O,B,E三点的二次函数关系式;
(2)求直线DE的解析式和点M的坐标;
(3)若反比例函数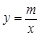 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=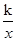 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).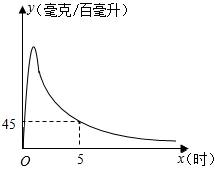
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
如图,直线 与反比例函数
与反比例函数 的图象在第一象限内交于A、B两点,交x轴的正半轴于C点,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为( )
的图象在第一象限内交于A、B两点,交x轴的正半轴于C点,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为( )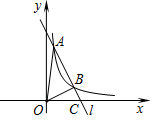
A.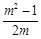 B.
B.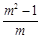 C.
C.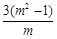 D.
D.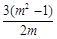
问题:如图,在 中, , , , 的平分线 , 分别与直线 交于点 , ,求 的长.
答案: .
探究:(1)把"问题"中的条件" "去掉,其余条件不变.
①当点 与点 重合时,求 的长;
②当点 与点 重合时,求 的长.
(2)把"问题"中的条件" , "去掉,其余条件不变,当点 , , , 相邻两点间的距离相等时,求 的值.
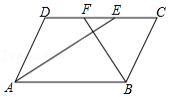
如图,在矩形 中, , ,将此矩形折叠,使点 与点 重合,点 落在点 处,折痕为 ,则 的长为 , 的长为 .
如图, 的直角边 在 轴上,顶点 的坐标为 ,直线 交 于点 ,交 轴于点 .
(1)求直线 的函数表达式;
(2)动点 在 轴上从点 出发,以每秒1个单位的速度向 轴正方向运动,过点 作直线 垂直于 轴,设运动时间为 .
①点 在运动过程中,是否存在某个位置,使得 ,若存在,请求出点 的坐标;若不存在,请说明理由;
②请探索当 为何值时,在直线 上存在点 ,在直线 上存在点 ,使得以 为一边, , , , 为顶点的四边形为菱形,并求出此时 的值.

如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A(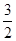 ,-2),反比例函数y=
,-2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.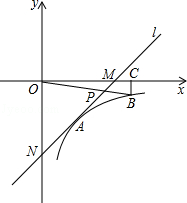
(1)求直线l的解析式;
(2)在函数y= (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
如图,在函数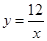 (x>0)的图象上,有点
(x>0)的图象上,有点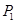 ,
,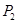 ,
, ,…,
,…,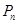 ,
,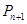 ,若
,若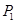 的横坐标为a,且以后每点的横坐标与它前面一个点的横坐标的差都为2,过点
的横坐标为a,且以后每点的横坐标与它前面一个点的横坐标的差都为2,过点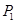 ,
,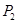 ,
, ,…,
,…,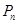 ,
,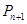 分别作x轴、y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为
分别作x轴、y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为 ,
,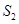 ,
,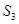 ,…,
,…,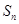 ,则
,则 = ,
= ,  +
+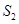 +
+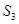 +…+
+…+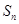 = .(用n的代数式表示)
= .(用n的代数式表示)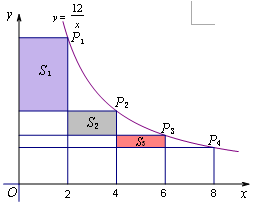
试题篮
()