如图,在平面直角坐标系中,反比例函数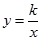 (
(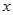 >0)的图象和矩形ABCD的第一象限,AD平行于
>0)的图象和矩形ABCD的第一象限,AD平行于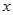 轴,且AB=2,AD=4,点A的坐标为(2,6) .
轴,且AB=2,AD=4,点A的坐标为(2,6) .
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
(本题12分)阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。如对于任意正实数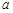 、x,可作变形:x+
、x,可作变形:x+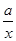 =(
=(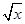 -
-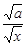 )2+2
)2+2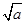 ,因为(
,因为(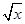 -
-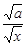 )2≥0,所以x+
)2≥0,所以x+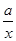 ≥2
≥2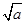 (当x=
(当x=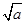 时取等号).
时取等号).
记函数y=x+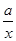 (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=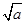 时,该函数有最小值为2
时,该函数有最小值为2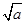 .
.
直接应用: 已知函数y1=x(x>0)与函数y2 = 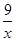 (x>0),则当x= 时,y1+y2取得最小值为 .
(x>0),则当x= 时,y1+y2取得最小值为 .
变形应用: 已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求 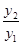 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
实际应用:汽车的经济时速是指汽车最省油的行驶速度。某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(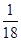 +
+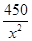 )升。若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升。若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
①求y关于x的函数关系式(写出自变量x的取值范围);
②求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
如图所示,已知A(  ,
,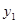 ),B(2,
),B(2,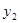 )为反比例函数
)为反比例函数 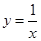 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )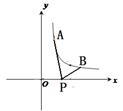
A.(  ,0) ,0) |
B.(1,0) | C.(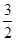 ,0) ,0) |
D.(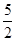 ,0) ,0) |
如图,已知直线y=4-x与反比例函数y=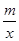 (m>0,x>0)的图象交于A、B两点,与x轴、y轴分别相交于C、D两点.
(m>0,x>0)的图象交于A、B两点,与x轴、y轴分别相交于C、D两点.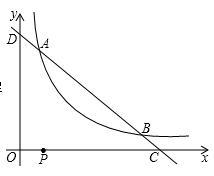
(1)如果点A的横坐标为1,利用函数图象求关于x的不等式4-x<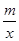 的解集;
的解集;
(2)如果点A的横坐标仍然为1,是否存在以AB为直径的圆经过点P(1,0)?若存在,求出m的值;若不存在,请说明理由.
如图,点P是反比例函数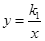 (k1>0,x>0)图象上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数
(k1>0,x>0)图象上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数 (k2<0且|k2|<k1)的图象于E、F两点.
(k2<0且|k2|<k1)的图象于E、F两点.
(1)图1中,四边形PEOF的面积S1= (用含k1、k2的式子表示);
(2)图2中,设P点坐标为(2,3).
①点E的坐标是( , ) ;点F的坐标是( , )(用含k2的式子表示);
②若△OEF的面积为 ,求反比例函数
,求反比例函数 的解析式.
的解析式.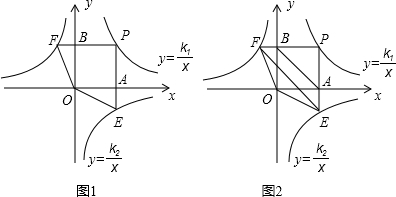
如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=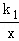 和y=
和y= 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①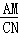 =
=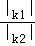 ; ②阴影部分面积是
; ②阴影部分面积是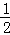 (k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )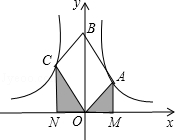
A.①②③ B.②④ C.①③④ D.①④
如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE。若OD=5,tan∠COD=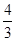 。
。
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形,若存在,请直接写出P点的坐标。若不存在,请说明理由;
一次函数y=ax+b与反比例函数 的图象交于A、B两点.过A点分别作x轴、y 轴的垂线,E、F为垂足.
的图象交于A、B两点.过A点分别作x轴、y 轴的垂线,E、F为垂足.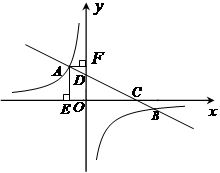
(1)请直接写出矩形AEOF的面积;
(2)设一次函数y=ax+b与x轴、y轴的交点分别为C、D,当OC=3OE时.
①试求△OCD的面积;
②当OE=1时,以BD为直径作⊙N,与x轴相交于P点,请求出P点的坐标.
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数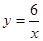 (x>0)的图像上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,……以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
(x>0)的图像上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,……以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )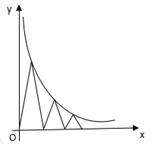
A.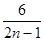 |
B.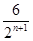 |
C. |
D.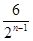 |
如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数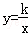 (x>0)图象上,△BOC的面积为8.
(x>0)图象上,△BOC的面积为8.
(1)求反比例函数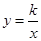 的关系
的关系
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式?
(3)当运动时间为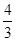 秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数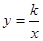 的图象经过点C,一次函数y=ax+b的图象经过点A.C
的图象经过点C,一次函数y=ax+b的图象经过点A.C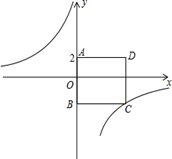
(1)求反比例函数和一次函数的解析式
(2)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,请直接写出P点的坐标.
如图,直线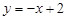 与反比例函数
与反比例函数 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.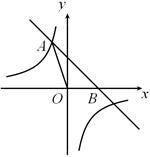
(1)求该反比例函数的表达式;
(2)若P为y轴上的点,且△AOP的面积是△AOB的面积的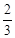 ,请求出点P的坐标.
,请求出点P的坐标.
(3)写出直线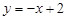 向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
在平面直角坐标系xoy中,对于点P(x,y),其中y≠0,我们把点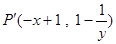 叫做点P的衍生点.已知点
叫做点P的衍生点.已知点 的衍生点为
的衍生点为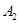 ,点
,点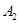 的衍生点为
的衍生点为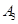 ,点
,点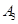 的衍生点为
的衍生点为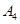 ,…,这样依次得到点
,…,这样依次得到点 ,
,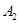 ,
,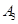 ,…,
,…,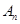 ,…,如果点
,…,如果点 的坐标为(2,-1),那么点
的坐标为(2,-1),那么点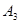 的坐标为________;如果点
的坐标为________;如果点 的坐标为(a,b),且点
的坐标为(a,b),且点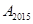 在双曲线y=
在双曲线y=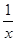 上,那么
上,那么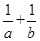 =________.
=________.
如图,直线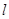 和双曲线
和双曲线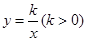 交于
交于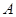 ,
,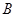 两点,
两点,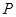 是线段
是线段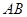 上的点(不与
上的点(不与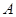 ,
,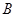 重合),过点
重合),过点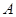 ,
,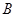 ,
,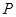 分别向
分别向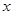 轴作垂线,垂足分别是
轴作垂线,垂足分别是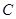 ,
, 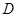 ,
,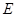 ,连接
,连接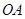 ,
,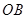 ,
,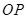 ,设
,设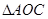 面积是
面积是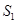 ,
,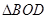 面积是
面积是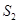 ,
,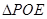 面积是
面积是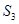 ,则( ).
,则( ).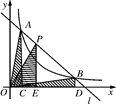
A.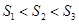 |
B.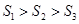 |
C.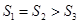 |
D. |
试题篮
()