如图,直线y=2x与双曲线 在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为
在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为
| A.(1.0) | B.(1.0)或(﹣1.0) |
| C.(2.0)或(0,﹣2) | D.(﹣2.1)或(2,﹣1) |
一次函数y=kx+b(k≠0)与反比例函数 的图象在同一直角坐标系下的大致图象如图所示,则k、b的取值范围是
的图象在同一直角坐标系下的大致图象如图所示,则k、b的取值范围是
| A.k>0,b>0 | B.k<0,b>0 | C.k<0,b<0 | D.k>0,b<0 |
已知两点P1(x1,y1)、P2(x2,y2)在反比例函数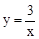 的图象上,当x1>x2>0时,下列结论正确的是【 】
的图象上,当x1>x2>0时,下列结论正确的是【 】
| A.0<y1<y2 | B.0<y2<y1 | C.y1<y2<0 | D.y2<y1<0 |
已知矩形的面积为8,则它的长y与宽x之间的函数关系用图象大致可以表示为
A. |
B. |
C. |
D. |
如图,已知直线y=mx与双曲线 的一个交点坐标为(3,4),则它们的另一个交点坐标是
的一个交点坐标为(3,4),则它们的另一个交点坐标是
| A.(﹣3,4) | B.(﹣4,﹣3) | C.(﹣3,﹣4) | D.(4,3) |
若反比例函数 的图象经过点(m,3m),其中m≠0,则此反比例函数图象经过
的图象经过点(m,3m),其中m≠0,则此反比例函数图象经过
| A.第一、三象限 | B.第一、二象限 | C.第二、四象限 | D.第三、四象限 |
已知梯形的面积一定,它的高为h,中位线的长为x,则h与x的函数关系大致是
A. |
B. |
C. |
D. |
如图,反比例函数 的图象上有一点A,AB平行于x轴交y轴于点B,△ABO的面积是1,则反比例函数的解析式是
的图象上有一点A,AB平行于x轴交y轴于点B,△ABO的面积是1,则反比例函数的解析式是
A. |
B. |
C. |
D. |
对于反比例函数 ,下列说法正确的是
,下列说法正确的是
| A.图象经过点(1,﹣3) | B.图象在第二、四象限 |
| C.x>0时,y随x的增大而增大 | D.x<0时,y随x增大而减小 |
如图,直线y=mx与双曲线 交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为
交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为
| A.﹣2 | B.2 | C.4 | D.﹣4 |
若ab>0,则一次函数y=ax+b与反比例函数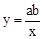 在同一坐标系数中的大致图象是
在同一坐标系数中的大致图象是
A.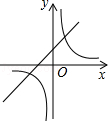 |
B.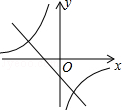 |
C.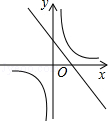 |
D.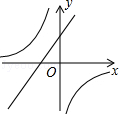 |
试题篮
()