初中数学平行线分线段成比例选择题

下列个命题中，是真命题的是（   ）

A．若x＞y，则x^2＞y^2

B．若（x1，y1）、（x2，y2）是函数图象上的两点，且x1＜x2，则y1＞y2

C．有两角及一边对应相等的两个三角形全等

D．对角线互相垂直的平行四边形是正方形

如图，在等腰△ABC中，AB=AC=4cm，∠B=30°，点P从点B出发，以cm/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BA-AC方向运动到点C停止，若△BPQ的面积为y（cm²），运动时间为x（s），则下列最能反映y与x之间函数关系的图象是（     ）

如图，反比例函数y=的图象经过点M，则此反比例函数的解析式为（     ）

A．y=-

B．y=

C．y=-

D．y=

如图，菱形OABC的顶点B在y轴上，顶点C的坐标为（﹣2，1），若反比例函数（x＞0）的图象经过点A，则k的值为（ ）

A．2

B．1

C．﹣1

D．﹣2

已知如图，A是反比例函数的图象上的一点，AB丄x轴于点B，且△ABO的面积是3，则k的值是（ ）

A．3

B．﹣3

C．6

D．﹣6

矩形的长为x，宽为y，面积为16，则y与x之间的函数关系用图象表示大致为（ ）

如图，点A在双曲线y=上，点B在双曲线y=上，且AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则它的面积为（ ）

A.1 B.2 C.3 D.4

下列各点中，在函数的图象上的是（ ）

A．（2，1）

B．（﹣2，1）

C．（2，﹣2）

D．（1，2）

给出以下四个命题：
①将一个n边形的纸片用剪刀剪去一个角（n≥4且剪裁线是直线），则剩下的纸片是n-1或n+1边；
②若x^-|x-3|=1，则x=1或3；
③已知函数y=（2k-3）x^k-3+是关于x的反比例函数，则k=；
④已知二次函数y=ax²+bx+c且a＞0，a-b+c＜0，则b²-4ac≤0．
其中正确的命题有（ ）

A．0个

B．1个

C．2个

D．3个

一次函数y=-kx+4与反比例函数的图象有两个不同的交点，点（-，y₁）、（-1，y₂）、（，y₃）是函数图象上的三个点，则y₁、y₂、y₃的大小关系是（ ）

A．y2＜y3＜y1	B．y1＜y2＜y3
C．y3＜y1＜y2	D．y3＜y2＜y1

在反比例函数y=的图象上有两点A（x₁，y₁）（x₂，y₂），当x₂＞x₁＞0时，有y₂＞y₁，则m的取值范围是（   ）

A．m＜0

B．m＞0

C．m＜

D．m＞

已知两点P₁（x₁，y₁）、P₂（x₂、y₂）在反比例函数y=的图象上，当x₁＞x₂＞0时，下列结论正确的是（   ）

A．0＜y1＜y2

B．0＜y2＜y1

C．y1＜y2＜0

D．y2＜y1＜0

如图，点A在双曲线y=上，点B在双曲线y=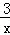上，且AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则它的面积为（ ）

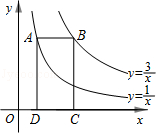
A．1        B．2        C．3        D．4

如图，双曲线y=经过点A（2，2）与点B（4，m），则△AOB的面积为（  ）．

A．2

B．3

C．4

D．5

如图，正比例函数y₁与反比例函数y₂相交于点E（﹣1，2），若y₁＞y₂＞0，则x的取值范围是（  ）．

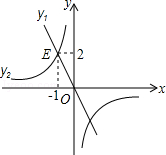
A．x＜﹣1

B．﹣1＜x＜0

C．x＞1

D．0＜x＜1