如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数 (x>0)的图象经过BC边上的中点D,交AB于点E.
(x>0)的图象经过BC边上的中点D,交AB于点E.
(1)k的值为_________;
(2)猜想△OCD的面积与△OBE的面积之间的关系,请说明理由.
(本题10分)已知反比例函数 的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
(1)求反比例函数的函数解析式;
(2)当四边形OADM的面积为2时,请判断BM与DM是否相等,并说明理由.
在平面直角坐标系 中,一次函数
中,一次函数 的图象与y轴交于点A,与x轴交于点B,与反比例函数
的图象与y轴交于点A,与x轴交于点B,与反比例函数 的图象分别交于点M、N,已知△AOB的面积为3,点M的纵坐标为4.
的图象分别交于点M、N,已知△AOB的面积为3,点M的纵坐标为4.
(1)求一次函数与反比例函数的解析式;
(2)求点N的坐标并直接写出当y1>y2时, 的取值范围.
的取值范围.
如图,在平面直角坐标系xoy中,一次函数 的图象与反比例函数
的图象与反比例函数 的图象的一个交点为A(-1,n).x轴上有点B,且△AOB的面积为3.
的图象的一个交点为A(-1,n).x轴上有点B,且△AOB的面积为3.
(1)求反比例函数 的解析式;
的解析式;
(2)求点B的坐标。
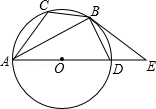
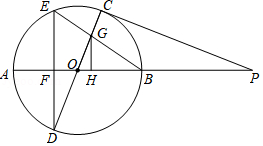
如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且 ,延长AD到E,且有 .
(1)求证:BE是⊙O的切线;
(2)若 , ,求圆的直径AD及切线BE的长.
如图,已知一次函数 与反比例函数
与反比例函数 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数 的图象,当
的图象,当 时,请直接写出自变量x的取值范围.
时,请直接写出自变量x的取值范围.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线 x+3交AB,BC分别于点M,N,反比例函数
x+3交AB,BC分别于点M,N,反比例函数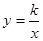 的图象经过点M,N.
的图象经过点M,N.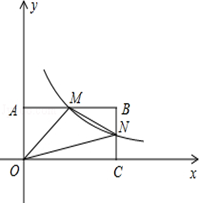
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
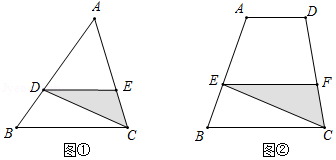
问题1:如图①,在 中, , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 的面积为 , 的面积为 .
(1)当 时, ;
(2)设 ,请你用含字母 的代数式表示 .
问题2:如图②,在四边形 中, , , , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 ,四边形 的面积为 , 的面积为 .请你利用问题1的解法或结论,用含字母 的代数式表示 .
如图,已知 , 是 的直径,过点 作 的切线交 的延长线于点 , 的弦 交 于点 ,且 .
(1)求证: ;
(2)连接 交 于点 ,过点 作 于点 ,若 , ,求 的长.
如图,在 中, ,点 从点 向点 运动,点 从点 沿射线 方向运动,且 ,连接 交 于 .
(1)如图1,当 时,求证: ;
(2)如图2,当 时,① , ,则 ;
②过点 作 于点 ,探究线段 , , 之间的数量关系,直接写出结论,不需证明.

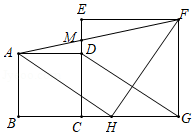
如图,正方形的边
在正方形
的边
上,连接
,过点
作
,交
于点
.连接
,
,其中
交
于点
.
(1)求证:为等腰直角三角形.
(2)若,
,求
的长.
已知一次函数 (m为常数)的图象与反比例函数
(m为常数)的图象与反比例函数  (k为常数,
(k为常数, )的图象相交于点 A(1,3).
)的图象相交于点 A(1,3).
(1)求这两个函数的解析式及其图象的另一交点 的坐标;
的坐标;
(2)观察图象,写出使函数值 的自变量
的自变量 的取值范围;
的取值范围;
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A( ,-2),反比例函数y=
,-2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l的解析式;
(2)在函数y= (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y= 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC= .
.
(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
试题篮
()