初中数学平行线分线段成比例解答题

已知正比例函数y=x和反比例函数的图象都经过点A（3，3）．

（1）直接写出反比例函数的解析式；
（2）把直线OA向下平移后与反比例函数的图象交于点B（6，m），求平移的距离．

甲、乙两家超市进行促销活动，甲超市采用“买100减50”的促销方式，即购买商品的总金额满100元但不足200元，少付50元；满200元但不足300元，少付100元；…．乙超市采用“打6折”的促销方式，即顾客购买商品的总金额打6折．
（1）若顾客在甲商场购买商品的总金额为x（100≤x＜200）元，优惠后得到商家的优惠率为p（p=），写出p与x之间的函数关系式，并说明p随x的变化情况；
（2）王强同学认为：如果顾客购买商品的总金额超过100元，实际上甲超市采用“打5折”、乙超市采用“打6折”，那么当然选择甲超市购物．请你举例反驳；
（3）品牌、质量、规格等都相同的某种商品，在甲乙两商场的标价都是x（300≤x＜400）元，认为选择哪家商场购买商品花钱较少？请说明理由．

如图，直线y=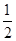x与双曲线y=（k＞0，x＞0）交于点A，将直线y=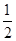x向上平移4个单位长度后，与y轴交于点C，与双曲线y=（k＞0，x＞0）交于点B．

（1）设点B的横坐标分别为b，试用只含有字母b的代数式表示k；
（2）若OA=3BC，求k的值．

已知反比例函数y₁=的图象与一次函数y₂=ax+b的图象交于点A（1，4）和点B（m，﹣2），

（1）求这两个函数的关系式；
（2）观察图象，写出使得y₁＞y₂成立的自变量x的取值范围；
（3）若P为Y轴上得一点，连接PA、PB，△PAB的面积为6，求P点的坐标。

如图，点A（m，6）、B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．

（1）求m、n的值并写出该反比例函数的解析式．
（2）点E在线段CD上，S_△ABE=10，求点E的坐标．

如图，一次函数的图象与x轴交于点B，与反比例函数的图象的交点为A（﹣2，3）．

（1）求反比例函数的解析式；
（2）过点A作AC⊥x轴，垂足为C，若点P在反比例函数图象上，且△PBC的面积等于18，求P点的坐标．

如图，点M（﹣3，m）是一次函数与反比例函数（）的图象的一个交点．

（1）求反比例函数表达式；
（2）点P是x轴正半轴上的一个动点，设OP=a（a≠2），过点P作垂直于x轴的直线，分别交一次函数，反比例函数的图象于点A，B，过OP的中点Q作x轴的垂线，交反比例函数的图象于点C，△ABC′与△ABC关于直线AB对称．
①当a=4时，求△ABC′的面积；
②当a的值为     时，△AMC与△AMC′的面积相等．

如图，反比例函数y=（k＜0）的图象与矩形ABCD的边相交于E、F两点，且BE=2AE，E（﹣1，2）．

（1）求反比例函数的解析式；
（2）连接EF，求△BEF的面积．

定义运算max{a，b}：当a≥b时，max{a，b}=a；当a＜b时，max{a，b}=b．如max{﹣3，2}=2．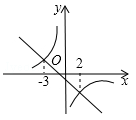

（1）max{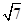，3}=     ；
（2）已知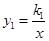和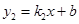在同一坐标系中的图象如图所示，若max{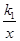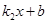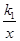，}=，结合图象，直接写出x的取值范围；
（3）用分类讨论的方法，求max{2x+1，x﹣2}的值．

（本题12分）如图，点B（2，2）在双曲线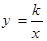（x＞0）上，点C在双曲线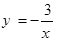（x＜0）上，点A是x轴上一动点，连接BC、AC、AB．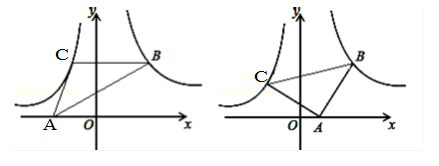

（1）求k的值；
（2）如图1，当BC∥x轴时，△ABC的面积；
（3）如图2，当点A运动到x轴正半轴时，若△ABC是等腰直角三角形，∠BAC=90°，求点A的坐标．

如图，反比例函数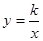的图象经过点（-1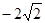，），点A是该图象第一象限分支上的动点，连结AO并延长交另一支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第四象限，AC与轴交于点P，连结BP．

（1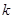）的值为   
（2）在点A运动过程中，当BP平分∠ABC时，点C的坐标是   

（本题10分）已知如图：点（1，3）在函数（x＞0）的图象上，矩形ABCD的边BC在x轴上，E是对角线BD的中点，函数（x＞0）的图象又经过A、E两点，点E的横坐标为m．

（1）求k的值；
（2）求点A的坐标；（用含m代数式表示）
（3）当∠ABD=45°时，求m的值．

如图，在平面直角坐标系中，已知点，反比例函数的图像经过点A，动直线与反比例函数的图像交于点M，与直线AB交于点N．

（1）求k的值；
（2）求△BMN面积的最大值；
（3）若,求t的值．

已知：一次函数的图象与反比例函数（）的图象相交于A，B两点（A在B的右侧）．

（1）当A（4，2）时，求反比例函数的解析式及B点的坐标；
（2）在（1）的条件下，反比例函数图象的另一支上是否存在一点P，使△PAB是以AB为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
（3）当A（a，﹣2a+10），B（b，﹣2b+10）时，直线OA与此反比例函数图象的另一支交于另一点C，连接BC交y轴于点D．若，求△ABC的面积．

平面直角坐标系中，点的横坐标的绝对值表示为，纵[坐标的绝对值表示为，我们把点的横坐标与纵坐标的绝对值之和叫做点的勾股值，记为：「」，即「」=+，（其中的“+”是四则运算中的加法）
（1）求点,的勾股值「」、「」
（2）点在反比例函数的图像上，且「」=4，求点的坐标；
（3）求满足条件「」=3的所有点围成的图形的面积