初中数学平行线分线段成比例解答题

已知函数y=y₁﹣y₂，且y₁为x的反比例函数，y₂为x的正比例函数，且和x=1时，y的值都是1．求y关于x的函数关系式．

如图，已知点P（a，b）、Q（b，c）是反比例函数y=在第一象限内的点，求的值．

已知点P（﹣1，n）在双曲线y=上．
（1）若点P（﹣1，n）在直线y=﹣3x上，求m的值；
（2）若点P（﹣1，n）在第三象限，点A（x₁，y₁），B（x₂，y₂）在双曲线上，且，试比较y₁，y₂的大小．

如图，在平面直角坐标系中，点是反比例函数图象上一点，⊥轴于点，一次函数的图象交轴于，交轴于点，并与反比例函数的图象交于两点，连接若△的面积为4，且．

(1) 分别求出该反比例函数和一次函数的解析式；
(2) 求△的面积.

已知：反比例函数和 在平面直角坐标系xOy第一象限中的图象如图所示，点A在的图象上，AB∥y轴，与的图象交于点B，AC、BD与x轴平行， 分别与、的图象交于点C、D.

（1）若点A的横坐标为2，求直线CD的解析式：
（2）若点A的横坐标为m，梯形ACBD的对角线的交点F，求的值．

如图，Rt△ABO的顶点A是双曲线与直线在第二象限内的交点，AB⊥轴于点B，且 .

（1）求这两个函数的表达式；
（2）求直线与双曲线的两个交点A、C的坐标；
（3）求△AOC的面积.

如图1，已知双曲线与直线交于A,B两点，点A在第一象限.试解答下列问题:
⑴若点A的坐标为（3，1），则点B的坐标为           ；
⑵当x满足：                        时，；
⑶过原点O作另一条直线l，交双曲线于P,Q两点，点P在第一象限， 如图2所示.
①四边形APBQ一定是                  ；
② 若点A的坐标为（3，1），点P的横坐标为1，求四边形APBQ的面积；

如图，已知A、B两点的坐标分别为A（0，2），B（2，0）直线AB与反比例函数y＝的图象交与点C和点D（－1，a）．

（1）求直线AB和反比例函数的解析式；
（2）求∠ACO的度数．

如图，已知直线经过点A(1，0)，与双曲线交于点B(2，1)．过点P(，－1)(其中＞1)作轴的平行线分别交双曲线和于点M、N．

（1）求的值；
（2）求直线的解析式；
（3）是否存在实数，使得S_△AMN＝4S_△AMP？若存在，请求出所有满足条件的的值；若不存在，请说明理由．

如图，函数的图象与反比例函数的图象的一个交点为A（1，m），点B（n，1）在反比例函数的图象上．

（1）求反比例函数的解析式；
（2）求n的值；
（3）若P是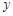轴上一点，且满足△POB的面积为6，求P点的坐标．

如图，⊿ACO的顶点A，C分别是双曲线与直线在第二象限、第四象限的交点，AB⊥轴于B且S_△ABO=

（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A，C的坐标；
（3）根据图象写出使的自变量x的取值范围.

(8分)如图，A、B两点在函数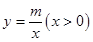的图象上.（1）求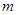的值及直线AB的解析式； （2）如果一个点的横、纵坐标均为整数，那么我们称这个点是格点.请直接写出图中阴影部分（不包括边界）中所有格点的坐标。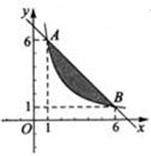

如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（4，2），过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N。

（1）求直线DE的解析式和点M的坐标；
（2）若反比例函数（x>0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上；
（3）若反比例函数（x>0）的图象与△MNB有公共点，请直接写出m的取值范围。

如图，过点B的直线l：交y轴于点A，与反比例函数的图象交于点C（2，n）和点D．



（1）求m和n的值，及另一交点D的坐标；
（2）求△COD的面积。

已知：如图，在平面直角坐标系中，直线与轴交于点，与反比例函数在第一象限内的图象交于点，连结，若．求该反比例函数的解析式和直线的解析式.