初中数学平行线分线段成比例解答题

如图所示，在平面直角坐标系中，一次函数y=kx+1，的图像与反比例函数的图像在第一象限相交于点A，过点A分别作x 轴、y轴的垂线，垂足为点B、C.如果四边形OBAC是正方形，求一次函数的关系式.

与成反比例，当＝2时，＝－1，求函数解析式和自变量的取值范围。

如图，反比例函数y＝(m≠0)与一次函数y＝kx＋b(k≠0)的图象相交于A、B两点，点A的坐标为(－6，2)，点B的坐标为(3，n)．求反比例函数和一次函数的解析式．

如图,一次函数与反比例函数在第一象限的图象交于点B，且点B的横坐标为1，过点B作轴的垂线，C为垂足，若，求一次函数和反比例函数的解析式.

如图，已知点A(－4，2)、B( n，－4)是一次函数的图象与反比例函数图象的两个交点．

(1) 求此一次函数的解析式和点B的坐标；
(2) 根据图象写出使一次函数的值小于反比例函数值的x的取值范围．

如图，一次函数y=kx+b与反比例函数的图象交于A（m，6），B（n，3）两点．
（1）求一次函数的解析式；
（2）根据图象直接写出时x的取值范围．

如图，直线l₁：与双曲线相交于点A（a，2），将直线l₁向上平移3个单位得到l₂，直线l₂与双曲线相交于B．C两点（点B在第一象限），交y轴于D点．
（1）求双曲线的解析式；
（2）求tan∠DOB的值．

如图，定义：若双曲线 (k＞0)与它的其中一条对称轴y＝x相交于A、B两点，则线段AB的长度为双曲线 (k＞0)的对径．
(1)求双曲线的对径．
(2)若双曲线 (k＞0)的对径是，求k的值．
(3)仿照上述定义，定义双曲线 (k＜0)的对径．

你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细（横截面积） s (mm²)的反比例函数，其图像如图所示。
（1）写出y与s的函数关系式；
（2）求当面条粗1.6mm²时，面条的总长度是多少米？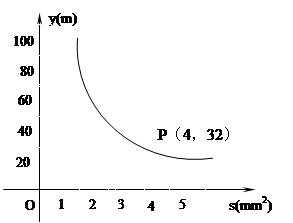

如图，己知双曲线y＝(x>0)与经过点A(1，0)、B(0，1)的直线交于P、Q两点，连结OP、OQ．
(1)求△OPQ的面积．
(2)试说明：△OAQ≌△OBP
(3)若C是OA上不与O、A重合的任意一点，CA＝a(0<a<1)，CD⊥AB于D，DE⊥OB于E．
①a为何值时，CE＝AC?
②线段OA上是否存在点C，使CE∥AB?若存在这样的点，请求出点C的坐标：若不存在，请说明理由．

如图，平面直角坐标系中，直线AB分别与轴交于点B、A，与反比例函数的图象分别交于点C、D，CE⊥轴于点E，点C坐标是（-2，3），点D的坐标是（6，n）.

（1）求一次函数和反比例函数的表达式；
（2）求△DCE的面积.

如图，已知反比例函数与一次函数的图象在第一象限相交于点．
（1）试确定这两个函数的表达式；
（2）连接OA、OB，求△AOB的面积．

如图，一次函数y＝kx＋b与反比例函数y＝的图象交于A（2，3），B（－3，n）两点．
（1）求一次函数与反比例函数的解析式；
（2）根据所给条件，请直接写出不等式kx＋b＞的解集；
（3）过点B作BC⊥x轴，垂足为C，求S_△ABC．

反比例函数的图象如图所示，，是该图象上的两点。
（1）比较与的大小；
（2）求的取值范围。

如图，正比例函数的图象与反比例函数在第一象限的图象交于点，过点作轴的垂线，垂足为，已知的面积为1.（1）求反比例函数的解析式；（2）如果为反比例函数在第一象限图象上的点（点与点不重合），且点的横坐标为1，在轴上求一点，使最小.