初中数学平行线分线段成比例解答题

已知反比例函数y=的图像经过点A(-，1)。
(1) 试确定此反比例函数的解析式；
(2) 点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB。判断点B是否在此反比例函数的图像上，并说明理由；
(3) 已知点P(m，m+6)也在此反比例函数的图像上(其中m<0)，过P点作x轴的垂线，交x轴于点M。若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n， 求n²-2n+9的值。

如图，一次函数的图象与反比例函数（x>0）的图象交于点P，PA⊥x轴于点A，PB⊥y轴于点B，一次函数的图象分别交x轴、y轴于点C、点D，且S_△DBP=27，。
（1）求点D的坐标；
（2）求一次函数与反比例函数的表达式；
（3）根据图象写出当x取何值时，一次函数的值小于反比例函数的值？

如图，反比例函数(k≠0)经过点A，连结OA，设OA与x轴的夹角为.
（1）求反比例函数解析式；
（2）若点B是反比例函数图象上的另一点，且点B的横坐标为sin,请你求出sin的值后，写出点B的坐标，并在图中画出点B的大致位置.

如图，已知反比例函数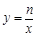（n＞0）与一次函数相交于A、B两点，AC⊥x轴于点C.若OC=1，且tan∠AOC＝3.点D与点C关于原点O对称。（1）求出反比例函数与一次函数的解析式；
（2）根据图像写出不等式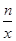＜kx+b的解集。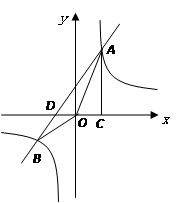

直线与反比例函数 (x>0)的图像交于点A，与坐标轴分别交于M、N两点，当AM=MN时,求k的值.

如图，一次函数的图象与反比例函数的图象相交于A、B两点．
（1）根据图象，分别写出A、B的坐标；
（2）求出两函数解析式；
（3）根据图象回答：当为何值时，一次函数的函数值大于反比例函数的函数值．

如图，反比例函数与一次函数的图象相交于A（1，3），B（n，–1）两点，求反比例函数与一次函数的解析式.

如图，一次函数的图象与反比例函数的图象相交于A、B两点．

（1）根据图象，分别写出A、B的坐标；
（2）求出两函数解析式；
（3）根据图象回答：当为何值时，一次函数的函数值大于反比例函数的函数值．

如图，一次函数的图像与反比例函数的图像交于两点，与轴交于点，与轴交于点，已知，点的坐标为，过点作轴，垂足为。
（1）求反比例函数和一次函数的解析式；
（2）求的面积。
（3）根据图像回答：当x 为何值时，一次函数的函数值大于
反比例函数的函数值？

直线与反比例函数 (x>0)的图像交于点A，与坐标轴分别交于M、N两点，当AM=MN时,求k的值.
                      

如图, 已知在平面直角坐标系中，一次函数(k≠0)的图象与反比例函数(m≠0)的图象相交于A、B两点，且点B的纵坐标为，过点A作AC⊥x轴于点C， AC=1,OC=2．
求：（1）求反比例函数和一次函数的关系式；
（2）直接写出反比例函数值大于一次函数值时x的取值范围.

如图，正比例函数的图象与反比例函数在第一象限的图象交于点，过点作轴的垂线，垂足为，已知的面积为1.

（1）求反比例函数的解析式；
（2）如果为反比例函数在第一象限图象上的点（点与点不重合），且点的横坐标为1，在轴上求一点，使最小.

如图，反比例函数（）与长方形在第一象限相交于、两点，,，连结、、．记、的面积分别为、．

（Ⅰ）①点坐标为    　　  ；
② 　（填“>”、“<”、“=”）；
（Ⅱ）当点为线段的中点时，求的值及点坐标；
（Ⅲ）当时，试判断的形状，并求的面积．

如图所示，过点作垂直轴的直线，分别交函数图象于两点，则　　　　　　．

（1）探究新知：如图1，已知△ABC与△ABD的面积相等， 试判断AB与CD的位置关系，并说明理由．

（2）结论应用：如图2，点M，N在反比例函数（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F． 试证明：MN∥EF．  
（3）变式探究：如图3，点M，N在反比例函数（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，过点M作MG⊥x轴，过点N作NH⊥y轴，垂足分别为E、F、G、H． 试证明：EF ∥GH．