初中数学平行线分线段成比例解答题

如图，直线l经过点A（1，0），且与曲线（x＞0）交于点B（2，1）．过点P（p，p－1）（p≥2）作x轴的平行线分别交曲线（x＞0）和（x＜0）于M，N两点．

求m的值及直线l的解析式；
是否存在实数p，使得S_△AMN=4S_△APM？若存在，请求出所有满足条件的p的值；若不存在，请说明理由

已知双曲线  与直线  相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线 上的动点．过点B作BD∥y轴交x轴于点D．过N（0，－n）作NC∥x轴交双曲线于点E，交BD于点C．
若点D坐标是（－8，0），求A、B两点坐标及k的值．
若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式．
在（2）的条件下，若P为x轴上一点，是否存在△OMP为等腰三角形？若存在，写出P点坐标；若不存在，说明理由。

如图，一次函数的图象与反比例函数的图象交于点P，点P在第一象限．PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交轴、轴于点C、D，且S_△PBD=4，．
求点D的坐标；
求一次函数与反比例函数解析式；
根据图象写出一次函数的值大于反比例函数的值的的取值范围.

已知反比例函数y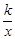＝的图象与一次函数y＝3x＋m的图象相交于点(1，5)．
求这两个函数的关系式．
求这两个函数图象的另一个交点的坐标

已知点A（-4，n）和点B（2，-4）是反比例函数的图象和一次函数 的图象的两个交点．

（1）求反比例函数和一次函数的解析式；
（2）求方程的解（请直接写出答案）；
（3）求不等式＞的解集（请直接写出答案）.

如图，一次函数y=" kx" +2的图象与x轴交于点B，与反比例函数y=的图象的一个交点为A(2，3)．
分别求出反比例函数和一次函数的解析式；
过点A作AClx轴，垂足为C，若点P在反比例函数图象上，且APBC的面积等于18，求P点的坐标．

已知，关于的方程（为整数）的根为整数，双曲线＞0过梯形的顶点和腰中点，如图所示，且∠,求四边形的面积。

如图，在平面直角坐标系xOy中，一次函数的图象与反比例函数 的图象的一个交点为A（-1，n）．（1）求反比例函数的解析式；（2）若P是坐标轴上一点，且PA=OA，试写出点的坐标．

如图，四边形OABC是面积为4的正方形，函数(x＞0)的图象经过点B．

(1)求k的值；
(2)将正方形OABC分别沿直线AB、BC翻折，得到正方形MABC′、MA′BC．设线段MC′、NA′分别与函数(x＞0)的图象交于点E、F，求线段EF所在直线的解析式．

已知：直线分别与 x轴、y轴交于点A、点B，点P（，b）在直线AB 上，点P关于轴的对称点P′ 在反比例函数图象上．
当a=1时，求反比例函数的解析式
设直线AB与线段P'O的交点为C．当P'C =2CO时，求b的值；
过点A作AD//y轴交反比例函数图象于点D，若AD=，求△P’DO的面积．

如图25，一次函数的图象与反比例函数的图象相交于A、B两点.
利用图中条件，求反比例函数和一次函数的解析式
根据图象写出使反比例函数的值大于一次函数的值的的取值范围  .

如图，D是反比例函数的图像上一点，过D作DE⊥x轴于E， DC⊥y轴于C，一次函数y=－x+m与y=－的图象都经过点C，与x轴分别交于A、B两点，四边形DCAE的面积为4，求k的值．

如图，在平面直角坐标系中，直线AB与反比例函数的图像交于点A(-3,4),AC⊥轴于点C.
求此反比例函数的解析式；
当直线AB绕着点A转动时,与轴的交点为B(a,0),并与反比例函数图象的另一支还有一个交点的情形下,求△ABC的面积S与之间的函数关系式.并写出自变量的取值范围．

如图,一次函数图象与x轴交于点A,与y轴交于点B,与双曲线的一支交于第二象限内一点C.

(1) 求字母n的取值范围;
(2) 若A(4,0),B(0,2),求一次函数解析式;
(3) 在(2)的情况下,若∠COB=∠CAO,求n的值.

如图，已知一次函数y₁ = k₁x + 6与反比例函数（x>0）的图象交于点A、B，且A、B两点的横坐标分别为2和4．
k₁= ▲ ，k₂= ▲ ；
求点A、B、O所构成的三角形的面积；
对于x>0，试探索y₁与y₂的大小关系（直接写出结果）．