如图,一次函数y=kx+b与反比例函数y= 的图象交于A(4,6),B(-6,n)两点.(1)求一次函数与反比例函数的解析式;
的图象交于A(4,6),B(-6,n)两点.(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b< 的解集______________;
的解集______________;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC. 
某工厂2011年1 月的利润为200万元.设2011年1 月为第1个月,第x个月的利润为y万元.由于排污超标,该厂从2011年1 月底起减产,并投入资金治污,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
(1)分别写出该化工厂治污期间及改造工程完工后y与x之间对应的函数关系式.
(2)治污改造工程顺利完工后经过1年,该厂利润能达到多少万元?
(3)当月利润少于100万元时为该厂资金紧张期,问该厂资金紧张期共有几个月?
已知反比例函数 图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB面积为3, 若直线y=ax+b经过点A,并且经过反比例函数
图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB面积为3, 若直线y=ax+b经过点A,并且经过反比例函数 的图象上另一点C(n,—
的图象上另一点C(n,— ),
),
(1)求反比例函数的解析式以及直线y=ax+b的解析式;
(2)求反比例函数的值大于一次函数的值时所对应的x的取值范围。
(3) 自己连接AC、和BC 并求△ABC的面积
选做题:本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
甲题:由山脚下的一点A测得山顶D的仰角是45°,从 沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
 |
乙题:如图,Rt△ABO的顶点A是双曲线 与直线
与直线 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO= .
.
求这两个函数的解析式
求直线与双曲线的两个交点A、C的坐标,并写出当x在什么范围取值时,
 y.
y.
在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.用列表法或画树状图表示出(x,y)的所有可能出现的结果
求小明、小华各取一次小球所确定的点(x,y)落在反比例函数
 的图象上的概率;
的图象上的概率;求小明、小华各取一次小球所确定的点(x,y)落在直线
 下方的概率.
下方的概率.
如图,在平面直角坐标系中,一次函数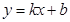 的图象与
的图象与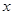 轴交于点
轴交于点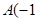 ,
,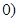 ,与反比例函数
,与反比例函数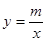 在第一象限内的图象交于点
在第一象限内的图象交于点 ,
,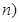 . 连结
. 连结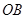 ,若
,若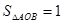 .
.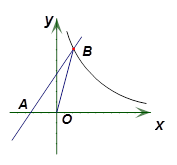
求反比例函数与一次函数的关系式;
直接写出不等式组
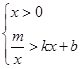 的解集.
的解集.
如图,直线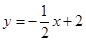 与
与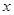 轴交于
轴交于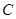 ,与
,与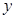 轴交于
轴交于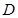 ,以
,以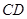 为边作矩形
为边作矩形 ,点
,点 在
在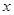 轴上,双曲线
轴上,双曲线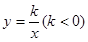 经过点
经过点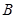 与直线
与直线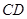 交于
交于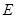 ,
,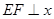 轴于
轴于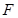 ,则
,则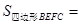 .
.
已知双曲线 和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.求双曲线
 的解析式;
的解析式;当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线
 另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
如图,一条直线与反比例函数y1= 的图象交于A(1,5),B(5,n)两点,与x轴交于D点, AC⊥x轴,垂足为C.
的图象交于A(1,5),B(5,n)两点,与x轴交于D点, AC⊥x轴,垂足为C.
(1)如图甲,①求反比例函数的解析式;②求n的值及D点坐标.
(2)如图乙,若点E在线段AD上运动,连结CE,作∠CEF=45°,EF交AC于F点.
①试说明△CDE∽△EAF;
②当△ECF为等腰三角形时,请求出F点的坐标.
如图,矩形OABC的顶点B点坐标为(3,2),点D是BC的中点.
(1)将△ABD向左平移3个单位,则点D的对应点E的坐标为 ;
(2)若点E在双曲线y= 上,则k的值为 ,直线OE与双曲线的另一个交点F的坐标是 ;
上,则k的值为 ,直线OE与双曲线的另一个交点F的坐标是 ;
(3)若在y轴上有一动点P,当点P运动到何处时PB+PF的值最小?求出此时的P点坐标.
如图所示,已知正方形 的面积为9 ,点
的面积为9 ,点 在函数
在函数 的图象上,点
的图象上,点 (
( )是函数
)是函数 的图象上动点,过点
的图象上动点,过点 分别作
分别作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 、
、 ,若设矩形
,若设矩形 和正方形
和正方形 不重合的两部分的面积和为
不重合的两部分的面积和为 。
。
(1)求 点坐标和
点坐标和 的值;(2)写出
的值;(2)写出 关于
关于 的函数关系和
的函数关系和 的最大值。
的最大值。
已知一次函数的图象与反比例函数的图象交于点A(3,2)、B(-2, m).求这两个函数的关系式,并在同一坐标系(如图7)中画出这两个函数的图象;
观察(1)中两个函数的图象,写出使一次函数的值大于反比例函数的值时,自变量x的取值范围.

如图,一次函数y1=ax+2与反比例函数y2= 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C,与x轴交于点D.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C,与x轴交于点D.
(1)求a、k的值;
(2)过点A作AE⊥x轴于点E,若P为反比例函数图象的位于第一象限部分上的一点,且直线OP分△ADE所得的两部分面积之比为2∶7.请求出所有符合条件的点P的坐标;
(3)在(2)的条件下,请在x轴上找一点Q,使得△PQC的周长最小,并求出点Q的坐标.
学生生物小组有一块长30m,宽20m的矩形ABCD试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道如图1,要使种植面积为504m2.
问题探究:
(1)如图1,小道的宽应设计为多少m?
(2)若设计者将图1中纵向小道变成如图2所示的一条与横向小道等宽的小道,请你说明两小道重叠部分四边形EFGO是什么特殊的四边形?此时种植面积 (填变化或不变)
(3)若设计者将图1中小道边交叉点O落在矩形ABCD的对角线BD上,并建立如图3所示的直角坐标系,且满足OM=ON,请你求出点A的坐标及过点C的反比例函数的关系式.
试题篮
()