如图,在平面直角坐标系xOy中,△ABC的边AC在x轴上,边BC⊥x轴,双曲线y=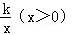 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).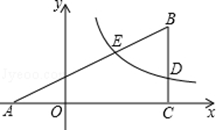
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC=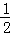 ,求k的值和点B的坐标.
,求k的值和点B的坐标.
(本小题满分8分)如图所示,反比例函数y1的图象经过点A(3,2),解答下列问题: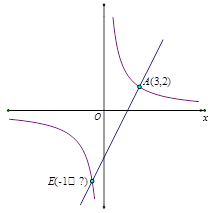
(1)求y1的函数关系式;
(2)过y1上任意一点B向x轴,y轴作垂线,交两坐标轴于C,D两点,求矩形OCBD的面积;
(3)过点A的一次函数y2与反比例函数y1的另一个交点E的横坐标为-1,求y2的关系式;
(4)通过图象回答当x取何值时,y1>y2;
直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=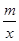 (x<0)交于点A(-1,n).
(x<0)交于点A(-1,n).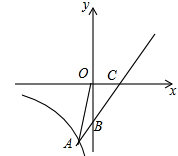
(1)求直线与双曲线的解析式.
(2)连接OA,求∠OAB的正弦值.
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由.
如图,已知正比例函数 和反比例函数的图象交于点A(m,-2).
和反比例函数的图象交于点A(m,-2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移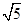 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
如图1,平面直角坐标系 中,等腰 的底边 在 轴上, ,顶点 在 的正半轴上, ,一动点 从 出发,以每秒1个单位的速度沿 向左运动,到达 的中点停止.另一动点 从点 出发,以相同的速度沿 向左运动,到达点 停止.已知点 、 同时出发,以 为边作正方形 ,使正方形 和 在 的同侧,设运动的时间为 秒 .
(1)当点 落在 边上时,求 的值;
(2)设正方形 与 重叠面积为 ,请问是否存在 值,使得 ?若存在,求出 值;若不存在,请说明理由;
(3)如图2,取 的中点 ,连结 ,当点 、 开始运动时,点 从点 出发,以每秒 个单位的速度沿 运动,到达点 停止运动.请问在点 的整个运动过程中,点 可能在正方形 内(含边界)吗?如果可能,求出点 在正方形 内(含边界)的时长;若不可能,请说明理由.
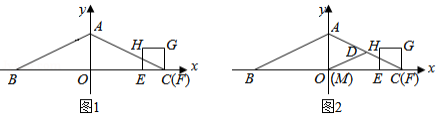
(本题满分 分)某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
分)某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
| X(元) |
3 |
4 |
5 |
6 |
| y(个) |
20 |
15 |
12 |
10 |
(1)根据表中的数据在平面直角坐标系中描出实数对(x,y)的对应点.
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
如图,在平面直角坐标系中,四边形ABCD是菱形,B、O在x轴负半轴上,AO=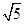 ,tan∠AOB=
,tan∠AOB=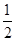 ,一次函数
,一次函数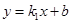 的图象过A、B两点,反比例函数
的图象过A、B两点,反比例函数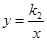 的图象过OA的中点D.
的图象过OA的中点D.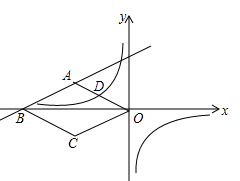
(1)求一次函数和反比例函数的表达式;
(2)平移一次函数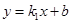 的图象,当一次函数
的图象,当一次函数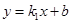 的图象与反比例函数
的图象与反比例函数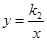 的图象无交点时,求b的取值范围.
的图象无交点时,求b的取值范围.
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2﹣18x+72=0的两根(OA>OC),BE=5,tan∠ABO=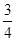 .
.
(1)求点A,C的坐标;
(2)若反比例函数y= 的图象经过点E,求k的值;
的图象经过点E,求k的值;
(3)若点P在坐标轴上,在平面内是否存在一点Q,使以点C,E,P,Q为顶点的四边形是矩形?若存在,请写出满足条件的点Q的个数,并直接写出位于x轴下方的点Q的坐标;若不存在,请说明理由.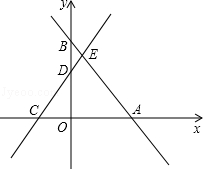
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题: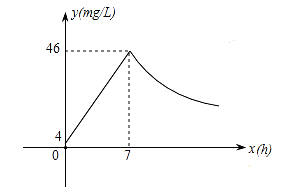
(1)求爆炸前与爆炸后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
问题:如图,在 中, , , , 的平分线 , 分别与直线 交于点 , ,求 的长.
答案: .
探究:(1)把"问题"中的条件" "去掉,其余条件不变.
①当点 与点 重合时,求 的长;
②当点 与点 重合时,求 的长.
(2)把"问题"中的条件" , "去掉,其余条件不变,当点 , , , 相邻两点间的距离相等时,求 的值.
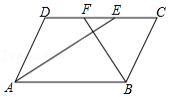
已知:如图,在菱形 中,点 、 分别在边 、 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 .
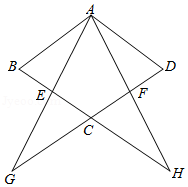
[小题1]求证: ;
[小题2]如果 ,求证: .
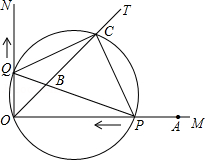
如图,已知 , 是 的平分线, 是射线 上一点, .动点 从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点 从点 出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点 .经过 、 、 三点作圆,交 于点 ,连接 、 .设运动时间为 ,其中 .
(1)求 的值;
(2)是否存在实数 ,使得线段 的长度最大?若存在,求出 的值;若不存在,说明理由.
(3)求四边形 的面积.
已知一次函数y=2x-k与反比例函数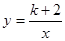 的图像相交于A和B两点.,如果有一个交点A的横坐标为3,
的图像相交于A和B两点.,如果有一个交点A的横坐标为3,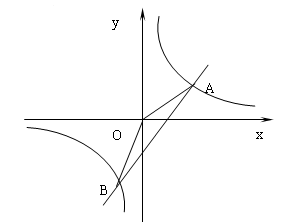
(1)求k的值;
(2)求A、B两点的坐标;
(3)根据图象写出一次函数的值大于反比例函数的值的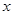 的取值范围
的取值范围
(4)求△AOB的面积;
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.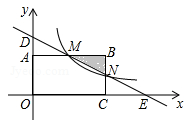
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数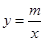 (x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
试题篮
()