如图,已知抛物线 经过O(0,0),A(4,0),B(3,
经过O(0,0),A(4,0),B(3, )三点,连接AB,过点B作BC∥
)三点,连接AB,过点B作BC∥ 轴交该抛物线于点C.
轴交该抛物线于点C.

求这条抛物线的函数关系式.
两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中,点P沿着线段0A向A点运动,点Q沿着线段AB向B点运动. 设这两个动点运动的时间为
 (秒) (0<
(秒) (0< ≤2),△PQA的面积记为S.
≤2),△PQA的面积记为S.
① 求S与 的函数关系式;
的函数关系式;
② 当 为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
是否存在这样的
 值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
(10’)设xi(i=1,2,3, ,n)为任意代数式,我们规定:y=max{x1,x2,x3,…,xn}表示x1,x2,…,xn中的最大值,如y=max{1,2}=2.
(1)求y=max{x,3};
(2)借助函数图象,解决以下问题:
①解不等式 max{x+1,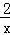 }≥2;
}≥2;
②若函数y=max{|x﹣1|,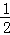 x+a,x2﹣4x+3}的最小值为1,求实数a的值.
x+a,x2﹣4x+3}的最小值为1,求实数a的值.
(11·贺州)
如图,在平面直角坐标系中,点O为原点,反比例函数 的图象经过点(1,4),菱
的图象经过点(1,4),菱
形OABC的顶点A在函数的图象上,对角线OB在x轴上.
(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线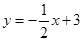 交AB,BC于点M,N,反比例函数
交AB,BC于点M,N,反比例函数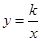 的图象经过点M,N.
的图象经过点M,N.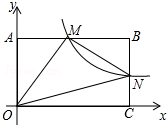
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.
如图,一次函数y=ax+b与反比例函数y=的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为 ,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.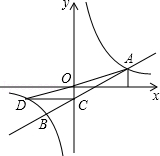
(1)求一次函数与反比例函数的解析式;
(2)求四边形OCBD的面积.
给出下列命题:
命题1:直线 与双曲线
与双曲线 有一个交点是(1,1);
有一个交点是(1,1);
命题2:直线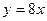 与双曲线
与双曲线 有一个交点是(
有一个交点是( ,4);
,4);
命题3:直线 与双曲线
与双曲线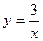 有一个交点是(
有一个交点是( ,9);
,9);
命题4:直线 与双曲线
与双曲线 有一个交点是(
有一个交点是( ,16);
,16);
……………………………………………………
(1)请你阅读、观察上面命题,猜想出命题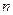 (
(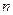 为正整数);
为正整数);
(2)请验证你猜想的命题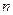 是真命题.
是真命题.
如图,在平面直角坐标系xOy中,△ABC的边AC在x轴上,边BC⊥x轴,双曲线y=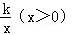 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).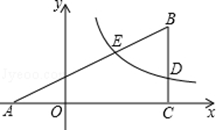
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC=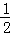 ,求k的值和点B的坐标.
,求k的值和点B的坐标.
问题:如图,在 中, , , , 的平分线 , 分别与直线 交于点 , ,求 的长.
答案: .
探究:(1)把"问题"中的条件" "去掉,其余条件不变.
①当点 与点 重合时,求 的长;
②当点 与点 重合时,求 的长.
(2)把"问题"中的条件" , "去掉,其余条件不变,当点 , , , 相邻两点间的距离相等时,求 的值.
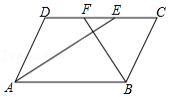
已知:如图,在菱形 中,点 、 分别在边 、 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 .
[小题1]求证: ;
[小题2]如果 ,求证: .
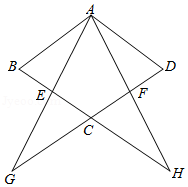
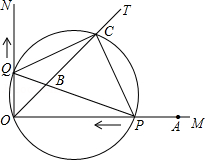
如图,已知 , 是 的平分线, 是射线 上一点, .动点 从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点 从点 出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点 .经过 、 、 三点作圆,交 于点 ,连接 、 .设运动时间为 ,其中 .
(1)求 的值;
(2)是否存在实数 ,使得线段 的长度最大?若存在,求出 的值;若不存在,说明理由.
(3)求四边形 的面积.
已知一次函数y=2x-k与反比例函数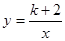 的图像相交于A和B两点.,如果有一个交点A的横坐标为3,
的图像相交于A和B两点.,如果有一个交点A的横坐标为3,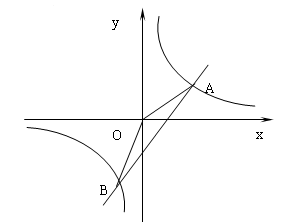
(1)求k的值;
(2)求A、B两点的坐标;
(3)根据图象写出一次函数的值大于反比例函数的值的 的取值范围
的取值范围
(4)求△AOB的面积;
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.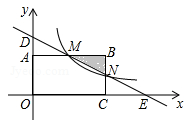
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数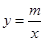 (x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
如图,已知反比例函数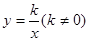 的图象经过点(
的图象经过点( ,8),直线
,8),直线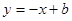 经过该反比例函数图象上的点Q(4,
经过该反比例函数图象上的点Q(4,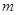 ).
).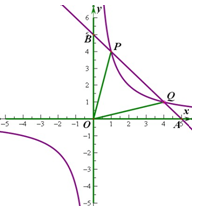
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与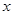 轴、
轴、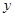 轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
试题篮
()