初中数学相似多边形的性质试题

如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．

（1）求证：∠B=∠D；
（2）若AB=4，BC﹣AC=2，求CE的长．

如图①，两个菱形ABCD和EFGH是以坐标原点O为位似中心的位似图形，对角线均在坐标轴上，已知菱形EFGH与菱形ABCD的相似比为1:2，∠BAD＝120°，其中AD＝4．
（1）点D坐标为     ，点E坐标为     ；
（2）固定图①中的菱形ABCD，将菱形EFCH绕O点顺时针方向旋转α度角（0°＜α＜90°），并延长OE交AD于P，延长OH交CD于Q，如图②所示，
①当α＝30°时，求点P的坐标；
②试探究：在旋转的过程中是否存在某一角度α，使得四边形AFEP是平行四边形？若存在，请推断出α的值；若不存在，说明理由；

如图，把含有30°角的三角板ABO置入平面直角坐标系中，A，B两点坐标分别为（3，0）和（0，3）．动点P从A点开始沿折线AO－OB－BA运动，点P在AO，OB，BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查，速度分别为1，，2 （长度单位/秒）﹒一直尺的上边缘l从x轴的位置开始以（长度单位/秒）的速度向上平行移动（即移动过程中保持l∥x轴），且分别与OB，AB交于E，F两点﹒设动点P与动直线l同时出发，运动时间为t秒，当点P沿折线AO－OB－BA运动一周时，直线l和动点P同时停止运动．

请解答下列问题：
（1）过A，B两点的直线解析式是   ；
（2）当t﹦4时，点P的坐标为    ；当t ﹦    ，点P与点E重合；
（3）① 作点P关于直线EF的对称点P′．在运动过程中，若形成的四边形PEP′F为菱形，则t的值是多少？② 当t﹦2时，是否存在着点Q，使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A，B，直线CD与x轴、y轴分别交于点C，D，AB与CD相交于点E，线段OA，OC的长是一元二次方程x²﹣18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=．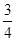
（1）求点A，C的坐标；
（2）若反比例函数y=的图象经过点E，求k的值；
（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．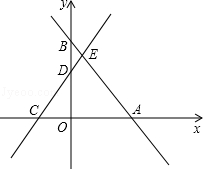

如图，在矩形ABCD中，AB=3，BC=4，动点P从点D出发沿DA向终点A运动，同时动点Q从点A出发沿对角线AC向终点C运动．过点P作PE∥DC，交AC于点E，动点P、Q的运动速度是每秒1个单位长度，运动时间为t秒，当点P运动到点A时，P、Q两点同时停止运动．

（1）用含有t的代数式表示PE=           ；
（2）探究：当t为何值时，四边形PQBE为梯形？
（3）是否存在这样的点P和点Q，使△PQE为等腰三角形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由．

已知梯形ABCD中，AD∥BC，AD=1，BC=2，sinB=，过点C在∠BCD的内部作射线交射线BA于点E，使得∠DCE=∠B．

（1）如图1，当ABCD为等腰梯形时，求AB的长；
（2）当点E与点A重合时（如图2），求AB的长；
（3）当△BCE为直角三角形时，求AB的长．

（本小题满分10分）已知AC，EC分别为四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90．

（1）如图①，当四边形ABCD和EFCG均为正方形时，连接BF．
i）求证：△CAE∽△CBF；
ii）若BE=1，AE=2，求CE的长；
（2）如图②，当四边形ABCD和EFCG均为矩形，且时，若BE＝1，AE=2，CE=3，求k的值；
（3）如图③，当四边形ABCD和EFCG均为菱形，且∠DAB=∠GEF=45°时，设BE=m，AE=n，CE=p，试探究m，n，p三者之间满足的等量关系．（直接写出结果，不必写出解答过程）

在△ABC中，点D在直线AB上，在直线BC上取一点E，连接AE，DE，使得 AE=DE，DE交AC于点G，过点D作DF∥AC，交直线BC于点F，∠EAC=∠DEF．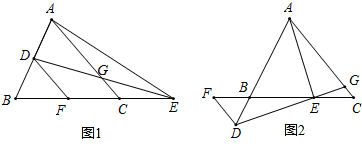

（1）当点E在BC的延长线上，D为AB的中点时，如图1所示．
①求证：∠EGC=∠AEC；
②若DF=3，求BE的长度；
（2）当点E在BC上，点D在AB的延长线上时，如图2所示，若CE=10，5EG=2DE，求AG的长度．

如图1，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，边AE上有一动点P（不与A，E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．

（1）直接写出 D，E 两点的坐标，D（         ），E（           ）
（2）求四边形PMNE的面积S与时间t之间的函数关系式；当t取何值时，S有最大值？
（3）当t为何值时，DP平分∠EDA？
（4）当t为何值时，以A，M，E为顶点的三角形为等腰三角形，并求出相应的时刻点M的坐标．

如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使得两个直角的顶点重合于对角线BD上一点P，EF、GH分别是折痕（如图2）．设AE＝x（0＜x＜2），给出下列判断：

①当x＝1时，点P是正方形ABCD的中心；
②当x＝时，EF＋GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确的是________（填序号）．

有两个直角三角板，在三角板ABC中，∠BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4，DE=4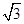，将这两个直角三角板按如图1所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上．现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动．
（1）如图2，当三角板DEF运动到点D到点A重合时，设EF与BC交于点M，则∠EMC=        度；
（2）如图3，当三角板DEF运动过程中，当EF经过点C时，求FC的长；
（3）在三角板DEF运动过程中，设BF=x，两块三角板重叠部分的面积为y，求y与x的函数解析式，并求出对应的x取值范围（直接写出结果，不必写过程）．

如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．
（1）问题发现
①当时，；
②当时， 
（2）拓展探究
试判断：当0°≤α＜360°时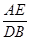，的大小有无变化？请仅就图2的情况给出证明．
（3）问题解决
当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长．

已知△ABC，延长BC到D，使CD=BC．取AB的中点F，连接FD交AC于点E．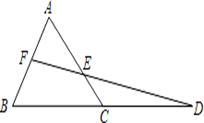

（1）求AE：AC的值；（2）若AB=a，FB=EC，求AC的长．

如图，在平面直角坐标系中，点A、C分别在x轴、y轴上，四边形ABCO为矩形，AB=16，点D与点A关于y轴对称，tan∠ACB=，点E、F分别是线段AD、AC上的动点（点E不与点A、D重合），且∠CEF=∠ACB．

（1）求AC的长和点D的坐标；
（2）说明△AEF与△DCE相似；
（3）当△EFC为等腰三角形时，求点E的坐标．

（年新疆区、兵团12分）如图，直线与x轴交于A点，与y轴交于B点，动点P从A点出发，以每秒2个单位的速度沿AO方向向点O匀速运动，同时动点Q从B点出发，以每秒1个单位的速度沿BA方向向点A匀速运动，当一个点停止运动，另一个点也随之停止运动，连接PQ，设运动时间为t（s）（0＜t≤3）．

（1）写出A，B两点的坐标；
（2）设△AQP的面积为S，试求出S与t之间的函数关系式；并求出当t为何值时，△AQP的面积最大？
（3）当t为何值时，以点A，P，Q为顶点的三角形与△ABO相似，并直接写出此时点Q的坐标．