如图,在Rt△ABC中,∠C=90°,CDEF为内接正方形,若AE=2cm,BE=1cm,则图中阴影部分的面积为
A、1cm2; B、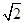 cm2; C、
cm2; C、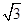 cm2; D、2cm2.
cm2; D、2cm2.
如图,在△ABC中,AB=AC=2,∠BAC=20°.动点P、Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( )

阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE,(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
| A.4米 | B.3.8米 | C.3.6米 | D.3.4米 |
如图,矩形 的四个顶点分别在菱形 的四条边上, .将 , 分别沿边 , 折叠,当重叠部分为菱形且面积是菱形 面积的 时,则 为
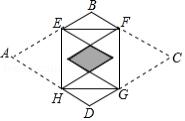
A. B.2C. D.4
如图,D、E分别在△ABC的边AB、AC上,要使△AED△与ABC相似,不能添加的条件是( )

A.DE∥BC B.AD•AC=AB•AE
C.AD:AC=AE:AB D.AD:AB=DE:BC
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(2,0),则点C的坐标为( )
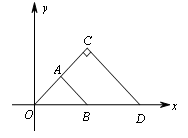
A.(2,2) B.(1,2) C.(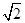 ,2
,2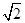 ) D.(2,1)
) D.(2,1)
小明一家人在国庆间自驾汽车从家里出发到某著名旅游景点游玩.他在1:500000的地图上测得家所在的城市与旅游景点所在城市的图上距离为40cm,则这两城市的实际距离为( )
| A.100km | B.200km | C.1000km | D.2000km |
若△ABC∽△A'B'C',∠A=40°,∠C=110°,则∠B'的度数为 ( )
| A.30° | B.50° | C.40° | D.70° |
如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且BD=3AD.那么AE:AC等于( )
A.2 : 3 B.1 : 2 C.1 : 3 D.1 :4
试题篮
()